Brøker

En brøk er en division, som man ikke har regnet helt ud. F.eks.

$$\frac{2}{7}$$

Tallet under brøkstregen kaldes nævneren, og tallet over brøkstregen kaldes tælleren. Regner man brøken ud, kaldes resultatet for kvotienten.

$$\frac{\text{Tæller}}{\text{Nævner}}=\text{Kvotient}$$

Det er vigtigt, at nævneren aldrig giver 0. (Hvordan skulle det give mening at dele noget i 0 stykker?)

Der er flere årsager til at skrive tal som brøker. Nogle gange er det fordi tallet vil have uendeligt mange decimaler som f.eks.

$$\frac{1}{3}=0,333333333.\,.\,.$$

Her kan det være praktisk at beholde brøken i stedet for at regne ud. Andre gange er det fordi, man gerne vil beskrive et forhold mellem to størrelser.

Brøkers størrelse

Hvis vi har en pizza er det klart, at jo flere stykker vi skærer den i, des mindre bliver stykkerne. Hvis pizzaen er skåret i 4 stykker repræsenterer hvert stykke 1/4, og hvis den er skåret i 8 stykker, repræsenterer hvert stykke 1/8

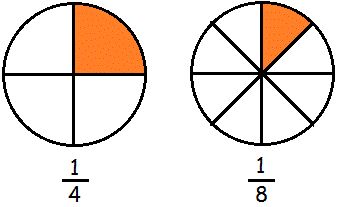
Det er tydeligt, at 1/8 er mindre end 1/4. Det vil altid være sådan, at jo større nævneren bliver, des mindre bliver kvotienten.

$$\text{Hvis}\quad m>n\quad \text{så er}\quad \frac{1}{m}<\frac{1}{n}$$

For at blive i pizzaeksemplet, kunne man spørge sig selv, hvor stor en del af pizzaen vi har, hvis vi har alle 8 stykker? Dette er selvfølgelig en hel pizza.

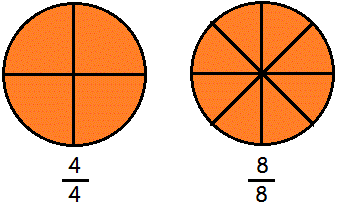
En brøk der har samme tæller og nævner, har altid kvotient 1

$$\begin{align*}\frac{8}{8}&=1\\\\\frac{4}{4}&=1\\\\\frac{n}{n}&=1,\:n\neq0\end{align*}$$

Videolektion