Fordoblings- og halveringskonstant
Når man har at gøre med en voksende eksponentiel funktion, så vil den vokse med en fast procent pr enhed på x-aksen. Efter et vist antal x-enheder vil den være vokset med 100% - dvs. den er fordoblet. Det stykke vi skal gå ud ad x-aksen, før funktionsværdien er fordoblet, kalder vi fordoblingskonstanten. Denne betegnes med T2
Grunden til, at der er tale om en konstant, er, at da udviklingen sker med en vis procent, så er det ligegyldigt, hvorhenne vi starter, da der stadig skal et lige langt stykke x-akse til at nå op på 100%.
Det kan virke lidt abstrakt, men prøv at se på følgende billede. Her er fordoblinskonstanten 3. Når vi går fra 0 til 3 på x-aksen, bliver y-værdien fordoblet (fra 4 til 8). Når vi går fra 7 til 10 på x-aksen bliver y-værdien imidlertid også fordoblet (fra 20 til 40).
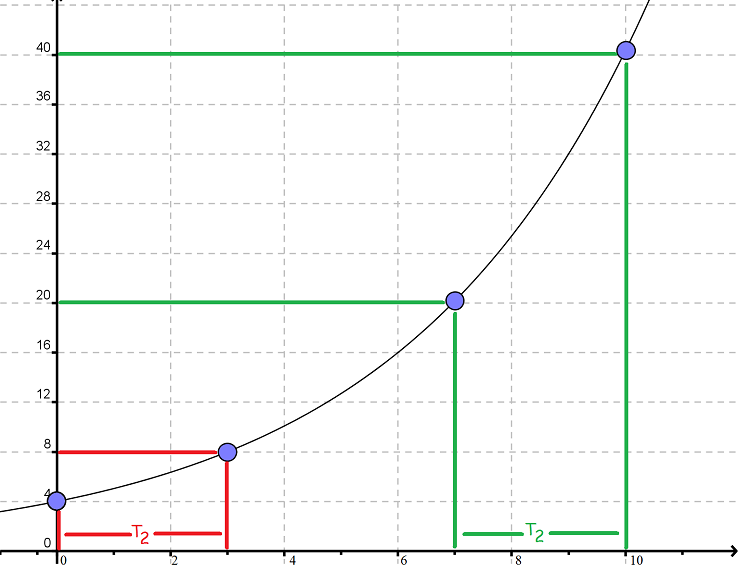
Men hvordan beregner vi så sådan en fordoblingskonstant? Lad os tage udgangspunkt i en eksponentialfunktion, der vokser med 26% for hvert x. Det betyder, at hver gang vi går 1 hen ad x-aksen, så skal vi gange med 1,26 på y-aksen.
Nu spørger vi os selv: Hvor mange gange skal vi gange med 1,26, før vi når op på 2 (en fordobling)?
| x-stigning | y-stigning |
| \(1\) | \(1,26\) |
| \(2\) | \(1,26\cdot1,26=1,5876\) |
| \(3\) | \(1,26\cdot1,26\cdot1,26=2\) |
Vi skal altså gå 3 skridt på x-aksen, før vi får fordoblet, og derfor er T2=3. Denne metode virkede kun, fordi vores fordoblingskonstant var et heltal. Generelt lyder
spørgsmålet: hvor mange gange skal man gange a med sig selv for at få 2? Eller udtrykt matematisk:
$$a^{T_2}=2$$
For at finde T2 bruger vi logaritmeregnereglerne
$$\log(a^{T_2})=\log(2)$$
$$T_2\cdot\log(a)=\log(2)$$
$$T_2=\frac{\log(2)}{\log(a)}$$
Altså kan vi finde fordoblingskontanten ved formlen
$$T_2=\frac{\log(2)}{\log(a)}$$
Hvis vores funktion således hedder
$$y=323\cdot1,12^x$$
kan vi altså beregne fordoblingskontanten som
$$T_2=\frac{\log(2)}{\log(a)}=\frac{\log(2)}{\log(1,12)}\approx6,12$$
Dvs. at lige meget hvor vi starter, så vil vores y-værdi blive fordoblet, når vi går 6,12 ud ad x-aksen.
Halveringskonstant
Ligesom de voksende eksponentialfunktioner har en fordoblingskonstant, så har de aftagende eksponentialfunktioner en halveringskonstant. Denne betegnes med T½
Her er der også tale om en konstant, da y-værdien aftager med en fast procent pr. x, og på et tidspunkt når man ned til 50% af det oprindelige.
På tegningen er halveringskonstanten 4.
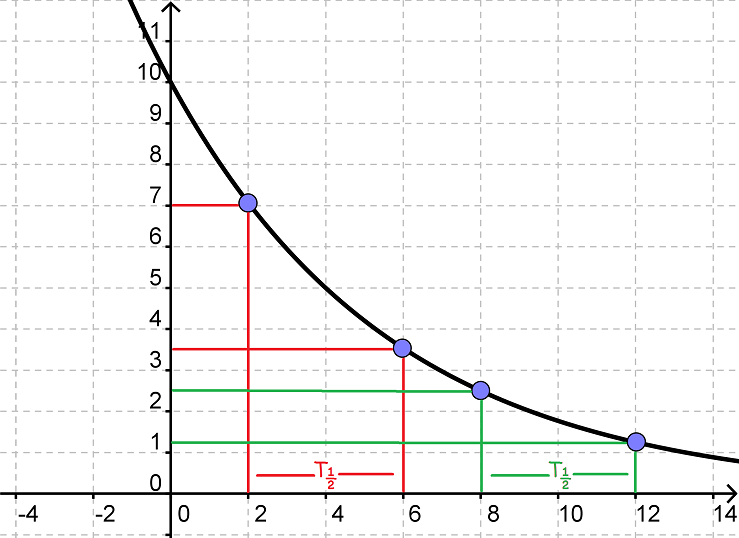
Når vi går 4 ud ad x-aksen fra 2 til 6, så bliver vores y-værdi halveret fra 7 til 3,5.
Og hvis vi var startet et andet sted f.eks. ved 8 og var gået 4 ud til 12, så ville vores y-værdi igen blive halveret, denne gang fra 2,5 til 1,25.
Lige meget, hvor vi var startet ville y-værdien halveres ved et 4trinsskridt på x-aksen. (F.eks. ville vi fra 0 til 4 halvere y-værdien fra 10 til 5).
Ligesom der fandtes en formel for fordoblingskonstanten, findes der også en for
halveringskonstanten. Her stiller man sig selv spørsmålet "hvor mange gange skal jeg gange a med sig selv for at få ½?".
$$a^{T_{\frac{1}{2}}}=\frac{1}{2}$$
Løsningen på denne ligning findes på samme måde som ved fordoblingskonstanten og er
$$T_\frac{1}{2}=\frac{\log(\frac{1}{2})}{\log(a)}$$
Hvis vores eksponentielle udvikling aftager med 10% (dvs a=0,90), så er halveringskontanten
$$T_\frac{1}{2}=\frac{\log(\frac{1}{2})}{\log(a)}=\frac{\log(\frac{1}{2})}{\log(0,90)}\approx6,58$$
Altså skal man gå 6,58 ud på x-aksen for at få halveret sin y-værdi.
Da eksponentialfunktioner ofte har at gøre med udvikling over tid, så kalder man til tider også fordoblingskonstanten for fordoblingstiden og halveringskonstanten for halveringstiden.
