Retvinklede trekanter og Pythagoras
En trekant, hvor en af vinklerne er 90º, kaldes retvinklet. Når man tegner en ret vinkel, plejer man at markere, at den er ret ved at tegne den firkantet i stedet for buet. Den side, der stå overfor den rette vinkel, kalder man hypotenusen, og de to sider, der er vinkelben for den rette vinkel, kaldes kateter.
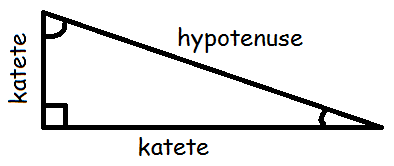
I retvinklede trekanter gælder Pythagoras' læresætning:
$$(1.\text{katete})^2+(2.\text{katete})^2=(\text{hypotenusen})^2$$
Du kender den måske snarere som
$$a^2+b^2=c^2$$
men hvis man skiver den på den måde, så er det vigtigt at gøre opmærksom på, at det er vinkel C, der er ret.
Hvis det f.eks. var vinkel A, der var ret, ville sætningen være:
$$b^2+c^2=a^2.$$
Hvis du vil se et eksempel på, hvor Pythagoras' læresætning bruges i virkeligheden, kan du klikke her.
Bevis for Pythagoras' læresætning
Man kan bevise Pythagoras' læresætning på mange måder. En af de letteste er ved hjælp af følgende tegning
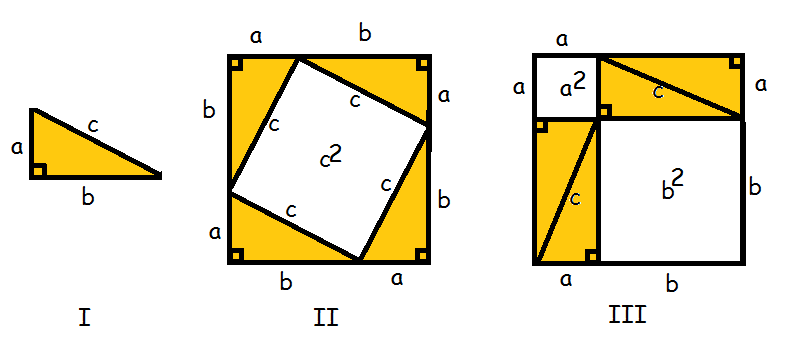
Vi betragter den retvinklede trekant ΔABC, hvor det er vinkel C, der er ret (I).
Vi tegner 4 af disse trekanter ind i et kvadrat med sidelængde a+b (II).
Den del af kvadratet, der ikke bliver dækket af trekanterne er selv et kvadrat med sidelængde c, og har derfor arealet
$$c\cdot c=c^2$$
Nu rykker vi rundt på de fire trekanter (III). Det område, der ikke er dækket af trekanterne danner to kvadrater. Det første har areal a2, det andet har b2.
Da vi bare har flyttet rundt på trekanterne mellem (II) og (III) må arealet af det udækkede område være uændret. Derfor er
$$a^2+b^2=c^2$$
