Grafisk løsning af to ligninger med to ubekendte
I nogle tilfælde kan man løse to ligninger med to ubekendte ved brug af grafer. Vi starter med at isolere den ene variable i begge ligninger. Derefter tegner vi de to grafer ind i et koordinatsystem. Koordinatsættene til skæringspunktet/-erne er løsningen/-erne til ligningssystemet.
Lad os se på et eksempel. Vores ligninger er
$$\begin{array}{rcl}
y & = & 3x+4\\
2x+y & = & 14.
\end{array}$$
Vi kan se at \(y\) allerede er isoleret i den første ligning. Så vi isolerer den blot i den anden ligning
$$\begin{array}{rcl}
2x+y & = & 14 \Leftrightarrow\\
y & = & -2x+14.
\end{array}$$
Nu tegner vi de to ligninger ind i et koordinatsystem
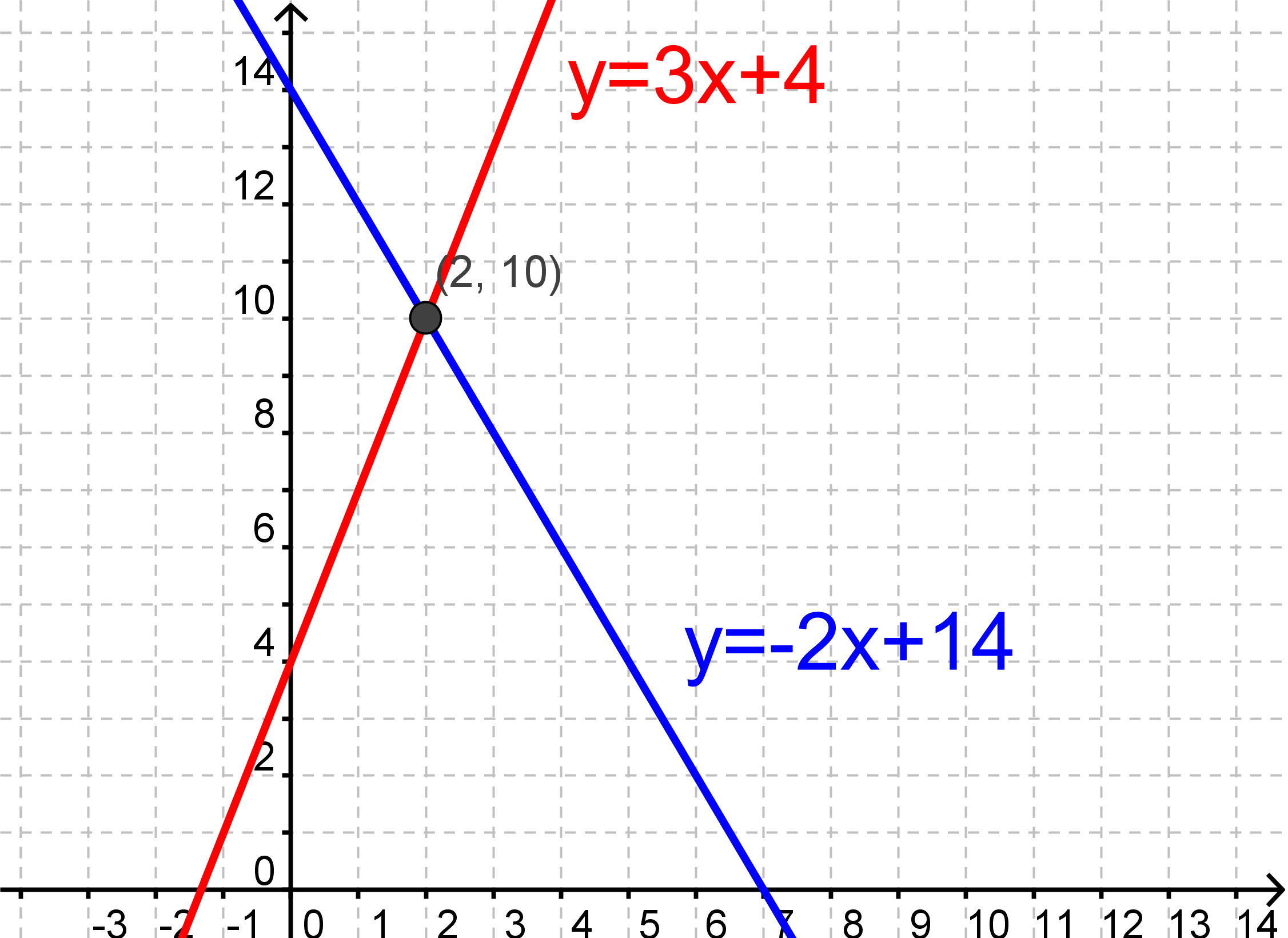
Vi kan se, at ligningerne har løsningen
$$x=2,\quad y=10$$
Vi prøver at sætte ind i de oprindelige ligninger for at sikre, at vi har regnet rigtigt. Indsættes løsningen i første ligning (\(y = 3x+4\)) får vi
$$\begin{array}{rl}
\mathrm{V}: & 10 = 10 \\
\mathrm{H}: & 3\cdot2+4 = 6+4 = 10.
\end{array}$$
samt for den anden ligning (\(2x+y=14\))
$$\begin{array}{rl}
\mathrm{V}: & 2\cdot 2+10 = 4 + 10 = 14\\
\mathrm{H}: & 14 = 14.
\end{array}$$
Lad os se på et andet eksempel. Vores ligninger er
$$\begin{array}{rcl}
2y+2x & = & 2x^2 \\
y-2x & = & 0
\end{array}$$
Vi starter med at isolere \(y\) i den første ligning
$$\begin{array}{rcl}
2y+2x & = & 2x^2 \Leftrightarrow\\
2y & = & 2x^2-2x \Leftrightarrow\\
y & = & x^2-x.
\end{array}$$
og så isolerer vi \(y\) i den anden ligning
$$\begin{array}{rcl}
y-2x & = & 0 \Leftrightarrow\\
y & = & 2x.
\end{array}$$
Nu indtegner vi graferne i et koordinatsystem
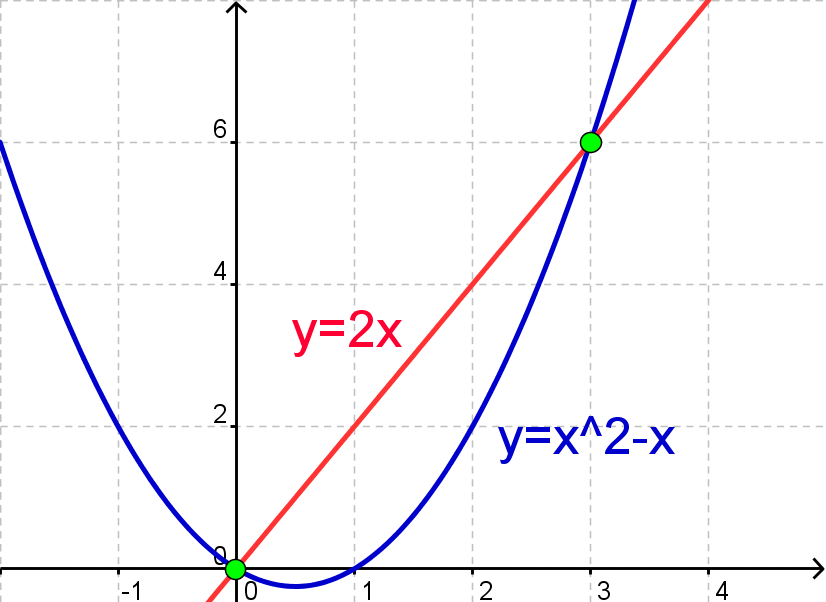
Vi aflæser skæringspunkterne til (0, 0) og (3, 6). Dvs. at en løsning er \(x=0\) og \(y=0\), mens en anden løsning er \(x=3\) og \(y=6\). For at sikre os, at vi har aflæst rigtig, prøver vi at indsætte punkterne i de oprindelige ligninger.
Først tjekker vi at (0, 0) er en løsning. For begge ligninger skal venstre og højre side af lighedstegnet give det samme
$$\begin{array}{rl}
\mathrm{V}: & 2y+2x = 2\cdot0+2\cdot0 = 0 \\
\mathrm{H}: & 2x^2 = 2\cdot0^2 = 2\cdot0 = 0.
\end{array}$$
og
$$\begin{array}{rl}
\mathrm{V}: & y-2x = 0-2\cdot0 = 0\\
\mathrm{H}: & 0 = 0.
\end{array}$$
Da venstre og højresiderne gav det samme i begge ligninger, er \(x=0\) og \(y=0\) en løsning. Nu ser vi på den anden løsning hvor \(x=3\) og \(y=6\)
$$\begin{array}{rl}
\mathrm{V}: & 2y+2x = 2\cdot6+2\cdot3=12+6=18 \\
\mathrm{H}: & 2x^2 = 2\cdot3^2 = 2\cdot9 = 18
\end{array}$$
samt
$$\begin{array}{rl}
\mathrm{V}: & y-2x = 6-2\cdot3 = 0\\
\mathrm{H}: & 0 = 0.
\end{array}$$
Igen får vi at højre- og venstresiderne stemmer overens i de to ligninger.
