Polynomium vs ligning
Der er forskel på et andengradspolynomium og en andengradsligning. Et andengradspolynomium er en funktion, hvor den højeste potens af \(x\) har eksponenten 2.
Forskriften ser således ud:
$$f(x)=ax^2+bx+c$$
For hver \(x\)-værdi, man kommer ind i polynomiet, finder man en y-værdi (en funktionsværdi). En andengradsligning derimod er - som navnet antyder - en ligning, hvor det handler om at finde de x-værdier, der løser ligningen. En andengradsligning har formen
$$ax^2+bx+c=0$$
Man skal altså finde ud af hvilke \(x\)-værdier, man kan sætte ind på venstresiden for at få 0.
At løse en andengradsligning svarer til at finde de \(x\)-værdier, hvor funktionsværdien (\(y\)-værdien) er 0 i andengradspolynomiet. Når \(y\) er 0, befinder vi os på \(x\)-aksen. Løsningerne til andengradsligningen er derfor skæringspunkterne mellem andengradspolynomiets graf og \(x\)-aksen. Nulpunkterne for et polynomium kaldes under tiden for polynomiets "rødder". Derfor kalder man tit løsningerne af en andengradsligning for det tilsvarende andengradspolynomiums rødder.
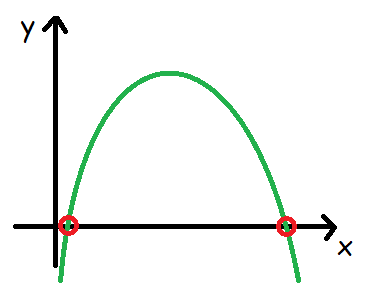
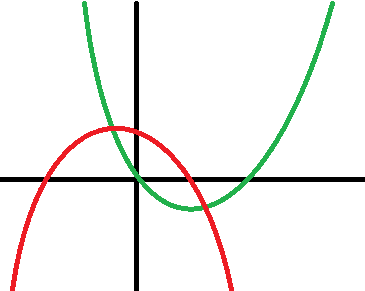
\(a\) og \(b\) kaldes koefficienterne til hhv. anden- og førstegradsleddet, mens \(c\) kaldes konstantleddet. Grafen for et andengradspolynomium kaldes en parabel. Man bruger tit betegnelserne "glad parabel" eller "sur parabel" alt efter hvilken vej, parabelbenene vender; om den ligner en sur eller en glad smiley. På tegningen herunder er den grønne parabel en glad parabel, mens den røde er sur.
Videolektion
I denne video vil vi forklare hvad forskellen på et polynomium og en ligning er samt til sidst giver vi nogle eksempler på disse.
