Stykkevise funktioner

Stykkevise funktioner er funktioner, hvor funktionsforskriften ændrer sig i forskellige intervaller. En stykkevis funktion kunne f.eks. se således ud:

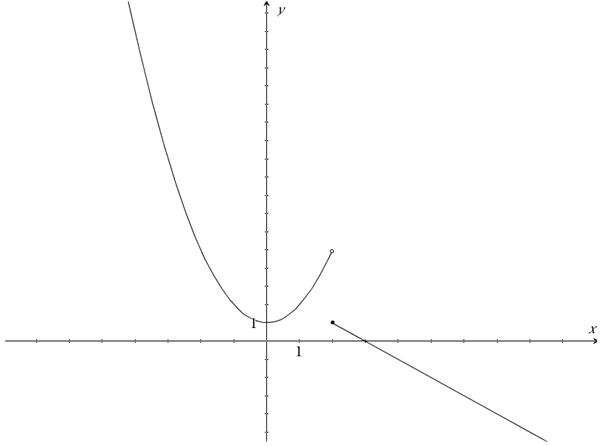
Vi ser, at denne kurve ikke er kontinuert, og at den skifter funktionsforskrift i punktet (2,1). Læg også mærke til, at punktet på enden af grafen for \(f(x)=x^2+1\) har en "åben bolle" - et punkt, der ikke er fyldt ud i midten. Dette markerer at \(x=2\) ikke ligger på grafen for \(x^2+1\). Den "lukkede bolle" i starten af grafen for \(f(x)=-3x+3\) markerer, at \(x=2\) er med på denne graf. 

Hvordan skrives de op? 

Funktionsforskriften for en stykkevis funktion skrives lidt anderledes, end man normalt er vant til. I funktionsforskriften er det nemlig vigtigt, at man definerer intervallerne, hvor de forskellige funktionsforskrifter er gældende. Dette kaldes også en gaffelforskrift. En funktion som den ovenfor kan skrives som.

$$f(x) = \begin{cases} x^2+1& \mathrm{for} \, x < 2\\ -x+3 & \mathrm{for} \, x \geq 2 \end{cases}$$

Differentiering af stykkevise funktioner

Når vi differentierer stykkevise funktioner, differentierer vi i virkeligheden bare i de forskellige intervaller hver for sig. Dette kan beskrives ved: 

$$f´(x) = \begin{cases} g´(x)\\ h´(x) \end{cases}$$

Vi ser her, at funktionen \(f(x)\) bliver differentieret ved, at differentiere de to funktioner \(g(x)\) og \(h(x)\) hver for sig. I dette eksempel har vi dog ikke defineret de intervaller, hvor \(g(x)\) og \(h(x)\) gælder i. Når vi definerer disse intervaller er det vigtigt at vide, at funktionen ikke er differentiabel i punktet eller punkterne, hvor funktionen bliver "splittet". I vores ovenstående tilfælde er funktionen \(f(x)\) altså ikke differentiabel i \(x=2\), selvom denne værdi er inkluderet i funktionen.