Multiplikations- og additionsprincipperne
Når man skal tælle kombinationer, er der nogle få regler, man skal huske på. Nogle af de vigtigste er multiplikations- og additionsprincipperne.
Multiplikationsprincippet
Hvis opgaven t1 kan udføres på m forskellige måder, og opgaven t2 kan udføres på n måder, så kan opgaven t1 og t2 udføres på m*n måder. Opgaven t1 eller t2 kan udføres på m+n måder.
Lad os tage et eksempel.
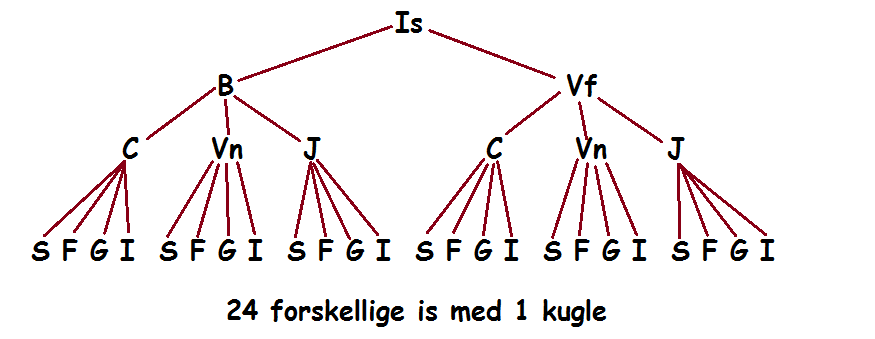
Vi går ind i en isbutik hvor vi vil have en is med 1 kugle.
- Man kan vælge, om man vil have i bæger eller vaffel.
- Man kan vælge mellem 3 slags is: chokolade, vanille og jordbær.
- Man kan vælge om man vil have: syltetøj, flødebolle, guf eller ingenting ovenpå.
På hvor mange måder kan man lave en is med 1 kugle?
Lad os kalde valget mellem bæger og vaffel for t1. Det kan udføres på 2 måder.
Lad os kalde valget af is for t2. Det kan udføres på 3 forskellige måder.
Lad os endelig kalde valget af topping for t3. Det kan udføres på 4 måder.
Da vi skal vælge en fra hver kategori, skal vi altså udføre t1 og t2 og t3. Derfor gør vi brug af multiplikationsprincippet. Vi skal altså gange antallet af muligheder med hinanden.
$$2\cdot3\cdot4=24$$
Vi har illustreret det med en tegning, hvor alle valgmulighederne fremstår ved at gå oppefra og ned.
Additionsprincippet
Hvis vi er lidt mere bestemte i vores valg af is, så kan vi se på hvor mange måder man kan lave en is med enten chokoladekugle eller flødebolle som topping. Det vil sige, hvor mange muligheder har vi, hvis vi godt kan lide chokoladekugle for sig og flødebolle som topping for sig, men ikke kan lide dem sammen.
Vi kalder antallet af muligheder med chokoladekugle for t1. Nu skal vi vælge 1 af de 2 type beholdere, iskuglen er allerede bestemt til at være chokolade, og dernæst 1 af de 3 slags topping (syltetøj, guf eller ingenting, men IKKE flødebolle). Altså kan t1 udføres på 6 (=2*1*3) måder.
Vi kalder antallet af muligheder med flødebolle for t2. Her kan vi igen vælge 1 af 2 beholdere, dernæst 1 af 2 typer is (vanille eller jordbær men IKKE chokolade), mens toppingen er forudbestemt til at være flødebolle. Altså kan t2 udføres på 4 (=2*2*1) måder.
Vi var interesserede i, at finde frem til, hvor mange måder, vi kunne vælge enten med flødebolle eller med én kugle chokoladeis. Altså t1 eller t2. Vi bruger additionsprincippet.
$$6+4=10$$
Der er altså 10 måder at lave en is med enten flødebolle eller chokoladeis.
De to principper ovenfor virker måske banale, men det er yderst vigtigt, du kan skelne mellem dem, når du skal udregne sandsynligheder i mere komplicerede tilfælde.
Hvis du vil se principperne anvendt, så kig på siden om kombinatorik og sandsynlighed!
