Monotoniforhold
At bestemme en funktions monotoniforhold svarer til at bestemme i hvilke intervaller, funktionen er voksende, og i hvilke, den er aftagende. Kender man monotoniforholdene, har man en idé om, hvordan grafen ser ud uden man behøver at tegne den. Differentialregning gør det meget lettere at bestemme monotoniforholdene.
Differentialkvotienten i et punkt x0 er lig med tangentens hældning i punktet (x0,f(x0), så derfor gælder det, at hvis differentialkvotienten er positiv i et punkt, vil tangenthældningen være positiv, og funktionen vil altså være voksende i det punkt. Hvis der er et åbent interval, hvor differentialkvotienten er positiv i alle punkter, så må alle tangenthældningerne altså være positive, og funktionen er derfor voksende på hele intervallet. På samme måde vil et interval med negative differentialkvotienter give et interval, hvor funktionen aftager. Hvis differentialkvotienten er 0 i et åbent interval, betyder det, at tangenthældningen er 0 (tangenten er vandret) og dermed er funktionen konstant på intervallet.
Ovenstående kan sammenfattes til det, der kaldes monotonisætningen:
$$f'(x)>0\:\text{for alle}\:x\in]a;b[\quad\Rightarrow\quad f\:\text{voksende på}\:[a;b]$$
$$f'(x)<0\:\text{for alle}\:x\in]a;b[\quad\Rightarrow\quad f\:\text{aftagende på}\:[a;b]$$
$$f'(x)=0\:\text{for alle}\:x\in]a;b[\quad\Rightarrow\quad f\:\text{konstant på}\:[a;b]$$
Maksimum, minimum og vendetangent
Det første, man gør, når man skal bestemme monotoniforholdene for en funktion, er at differentiere funktionen og sætte den afledede lig med 0. Man løser altså ligningen
$$f'(x)=0 \ .$$
De x-værdier, der løser denne ligning, er dem, hvor tangenten er vandret. Der er tre muligheder for, hvad disse punkter kan være. De kan være makismumspunkter, minimumspunkter eller vendetangentspunkter.
Imellem to punkter, hvor \(f '(x_0)=0\) er den enten positiv på hele intervallet eller negativ på hele intervallet. Hvis den skulle skifte mellem at være positiv og negativ ville den jo være nødt til at passere \(0\).
Altså kan vi undersøge, om \(f '(x_0)\) er positiv eller negativ i intervallerne mellem nulpunkterne ved bare at vælge et tilfældigt punkt i intervallet og se på fortegnet af \(f '\) i dette punkt.
Hvis \(f '(x_0)\) er positiv til venstre og negativ til højre for \(f '(x_0)\)=0, så er der tale om et maksimum.
Hvis \(f '(x_0)\) er negativ til venstre og positiv til højre for \(f '(x_0)\)=0, er der tale om et minimum.
I forbindelse med undersøgelse af en funktions monotoniforhold har vi normalt at gøre med funktioner, der er kontinuerte i hele deres definitionsmængde og dermed også i ethvert delinterval. For sådanne funktioner gælder det, at når de er kontinuerte i et lukket interval [a;b], så er funktionen voksende, aftagende eller eventuelt konstant i hele intervallet [a;b], altså inklusiv intervalendepunkterne, når blot \(f '(x)\) er positiv, negativ eller nul i hele det åbne interval ]a;b[. Dette er en konsekvens af, at kontinuerte funktioner har en sammenhængende graf, så funktionsværdierne \(f (a)\) og \(f (b)\) fastlægges af værdierne i det åbne interval ]a;b[, nemlig som grænseværdierne af \(f (x)\) for x gående mod henholdsvis a og b.
Hvis vi derfor for en funktion \(f (x)\) konstaterer, at \(f '(x)=0 ⇔ x=−2 ∨ x=0\) og at \(f '(x)>0\) for alle x i intervallet ]-2;0[, så er \(f(x)\) voksende i hele intervallet [-2;0], inklusiv endepunkterne og ikke bare i det åbne interval ]-2;0[ (se senere i det gennemregnede eksempel).
Hvis \(f '(x)\) har samme fortegn på begge sider af \( x_0 \) , så er \(f (x)\) voksende (fortegnsvariation: + 0 +) eller aftagende (fortegnsvariation: - 0 -) på begge sider af \( x_0 \) og grafen for \(f (x)\) har da en vandret tangent i punktet \((x_0,f(x_0)\). Denne tangent krydser gennem grafen, dvs. på den ene side ligger den over grafen og på den anden side ligger den under grafen. En sådan tangent kaldes en vendetangent. Et eksempel på denne situation forekommer i funktionen \(f(x)=(x−3)^3+2 \), som har en vandret vendetangent i punktet (3,2) (kontroller eventuelt selv dette).
Figuren nedenfor viser grafen for en funktion med et lokalt maksimum og et lokalt minimum (vandrette tangenter) og en vendetangent, men denne er ikke vandret som beskrevet ovenfor. Vendetangenter bliver typisk ikke introduceret på B-niveau, men først på A-niveau. Du kan folde siden ud nedenfor, hvis du vil læse om vendetangenter.
Vendetangenter vil typisk ikke blive introduceret på B-niveau, men først på A-niveau. Hvis vi forestiller os en tangent på figuren nedenfor starte helt ude til venstre på grafen, så vil den være ret stejl og have positiv hældning. Lader vi nu tangenten køre langs grafen vil den i starten stadig have positiv hældning, men hældningen bliver mindre og mindre, dvs. \(f '(x)\) opfattet som funktion er aftagende. Dette fortsætter lidt endnu også efter at tangenten har passeret den grønne tangent, men et eller andet sted mellem grafens to toppunkter begynder hældningen igen at blive større og større, først negativ frem til det lokale minimum og derefter igen positiv. Her er \(f '(x)\) opfattet som funktion altså voksende.
Endvidere konstaterer vi, at samtidig med at \(f '(x)\) skifter fra at være aftagende til at være voksende, så ”skærer” tangenten gennem grafen for \(f (x)\). Det kan ses som den blå tangent på grafen. Den x-værdi, \( x_0 \) , hvor skiftet sker, vil vi gerne finde. Tangenten i punktet \((x_0,f(x_0)\) kaldes en vendetangent.
Da \(f '(x)\) skifter fra at være aftagende til at være voksende i \( x_0 \) , må \(f '(x)\) have et lokalt minimum i \( x_0 \) , dvs. den afledede funktion til \(f '(x)\) må være nul, altså \(f ''(x)=0\). Kandidaterne til mulige vende- tangenter skal altså søges blandt løsningerne til denne ligning, og kravet til en kandidat er, at \(f '(x)\) har et toppunkt, lokalt maksimum eller lokalt minimum i \( x_0 \) .
At finde vendetangenter til grafen for en funktion \(f (x)\) kan altså ske ved at foretage en funktionsundersøgelse af den afledede funktion \(f '(x)\). Dette indebærer, at vi skal lave en fortegnsundersøgelse af den dobbelt afledede funktion \(f ''(x)\) efter helt samme opskrift, som vi tidligere lavede fortegnsundersøgelse af \(f '(x)\) for at bestemme monotoniforholdene for \(f (x)\).
Når vi løser ligningen \(f ''(x)=0\) giver det følgende fire muligheder for fortegnsvariationerne omkring nul- punkterne/løsningerne: + 0 - , - 0 +, + 0 + og - 0 -. De to første muligheder fører til henholdsvis et lokalt maksimum og et lokalt minimum for \(f '(x)\) i \( x_0 \) , dvs. vendetangenter i punktet \((x_0,f(x_0)\), mens de to sidste muligheder ikke giver en vendetangent, idet der ikke er lokale ekstrema til \(f '(x)\) i disse to tilfælde.
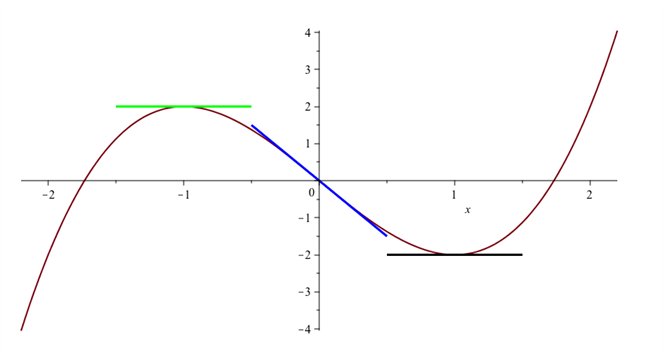
Grøn tangent er lokalt maksimum, sort tangent er lokalt minimum og blå tangent er vendetangent.
Eksempel
Vi ønsker at bestemme monotoniforholdene for funktionen
$$f(x)=-x^3-3x^2+2 \ .$$
\(f\) er en differentiabel funktion, så vi starter med at differentiere den
$$f'(x)=-3x^{3-1}-3\cdot2x^{2-1}+0=-3x^2-6x \ .$$
Nu ønsker vi at finde de x-værdier, hvor \(f '(x)\) er \(0\)
$$\begin{align}
0 &= f'(x) \Leftrightarrow\\
0 &= -3x^2-6x \Leftrightarrow\\
0 &= -3x(x+2) \ .
\end{align}$$
Nulreglen giver nu, at løsningerne er
$$x=0\quad\vee \quad x=-2 \ .$$
I disse to punkter er tangenten altså vandret. Vi undersøger fortegnet for \( f' \) i intervallerne mellem dem. Det er nok bare at se på et vilkårligt tal i hvert interval.
Lad os starte med et tal mindre end \(-2\). F.eks. \(-3\)
$$f'(-3)=-3\cdot(-3)^2-6\cdot(-3)=-3\cdot9+6\cdot3=-27+18=-9<0 \ .$$
Altså kan vi slutte
$$x<-2\quad\Rightarrow\quad f'(x)<0 \ .$$
Dette kan vi også sige som
$$f\text{ aftager når } x<-2 \ .$$
Så undersøger vi fortegnet af \(f ' \) når x ligger mellem \(-2\) og \(0\). Vi tager et tilfældigt tal i intervallet. Det kunne f.eks. være \(-1\),
$$f'(-1)=-3\cdot(-1)^2-6\cdot(-1)=-3\cdot1+6=3>0 \ .$$
Altså kan vi slutte, at
$$x\in[-2,0]\quad\Rightarrow\quad f'(x)>0 \ .$$
Dette kan vi også sige som
$$f\text{ vokser når } x\in[-2;0] \ .$$
Endelig ser vi på intervallet, hvor x er større end 0. Vi vælger et tilfældigt tal i dette interval. Det kunne f.eks. være 1,
$$f'(1)=-3\cdot1^2-6\cdot1=-3-6=-9<0 \ .$$
Altså kan vi slutte, at
$$x>0\quad\Rightarrow\quad f'(x)<0 \ .$$
Dette kan vi også sige som
$$f\text{ aftager når } x>0 \ .$$
Vi kan også tjekke, om funktionen har en vendetangent. Som tidligere omtalt finder vi vendetangenter ved at løse ligningen \(f''(x)=0\), hvor \(f''(x)\) er den anden afledede af \(f(x)\). Vi kender allerede \(f'(x)\) og differentierer derfor én gang til:
$$f''(x)=(−3x^2−6x)'=−6x−6$$
Løser ligningen:
$$f''(x)=0 \Leftrightarrow −6 x−6=0 \Leftrightarrow x=−1$$
Indsætter i \(f ''(x)\) en x-værdi fra hvert af intervallerne ]-∞;-1[ og ]-1;∞[ , f.eks. -2 og 0 og får:
$$f''(−2)=6 \quad \text{og} \quad f''(0)=−6$$
Heraf følger, at \(f ''(x)>0\) i intervallet ]-∞;-1[ og \(f ''(x)<0\) i intervallet ]-1;∞[ , og dermed er \(f '(x)\) voksende i intervallet ]-∞;-1] og aftagende i intervallet [-1;∞[ . Altså har \(f '(x)\) et toppunkt (her maksimum) i punktet \((-1,f(-1))\) og grafen for \(f (x)\) dermed en vendetangent i dette punkt, jf. de tidligere bemærkninger om vendetangenter. Da vi kender tangentens hældningskoefficient \(f '(-1)=3\) og røringspunktet (-1,0) kan tangentens ligning bestemmes. Resultat:
$$y=3 x+3$$
Monotonilinje
Vi kan tegne resultaterne ind i en monotonilinje.
Man tegner en tallinje. Ovenover den har man x, under den \(f '\) og \(f\).
Først tegner man de x-værdier ind, hvor \(f '(x)=0\). Man skriver derfor \(0\) ud for \(f '\) ved disse x-værdier. Dernæst indtegner man fortegnene for \(f '\) mellem disse værdier.
Til sidst tegner man pile alt efter, hvad det betyder for \(f\). Under et plus tegner man en pil der går opad mod højre og under et minus tegner man en pil, der går nedad mod højre. Når man har tegnet pilene kan man se, hvad der er lokale maksima og minima, og hvad der er vendetangenter. Her er monotonilinjen tegnet skridt for skridt for eksemplet herover.
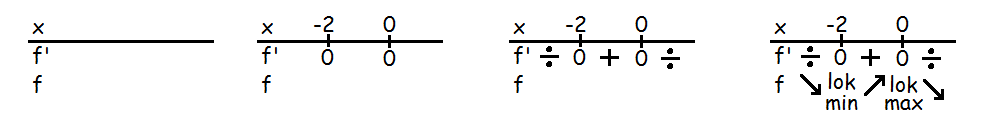
Man skal altid afslutte med at konkludere, hvordan monotoniforholdene er. I dette tilfælde ville man skrive:
$$f\text{ er aftagende på intervallerne }]-\infty;-2] \text{ og }[0;\infty[$$
$$f\text{ er voksende på intervallet } [-2;0]$$
$$f\text{ har lokalt minimum i }(-2, f(-2)) \text{ og lokalt maksimum i }(0,f(0)).$$
Herunder er \(f\) tegnet, så man kan se, at det er det rigtige, man er nået frem til

Opsummering
For at opsummere er der følgende opskrift, man altid kan følge for at finde monotoniforholdene for en funktion.
- Differentier funktionen
- Løs ligningen \(f '(x)=0\)
- Bestem fortegnet for \(f '(x)\) mellem nulpunkterne.
- Tegn monotonilinje
- Konkluder med tekst
