Grundrelationen

Grundrelationen er en sammenhæng mellem cosinus og sinus, som det er vigtigt at kunne. Man kan tit bruge den til at reducere udtryk. 

Den lyder sådan her:

$$(\cos(v))^2+(\sin(v))^2=1$$

Relationen gælder lige meget hvilken vinkel, man putter ind i cosinus og sinus (så længe det er den samme i begge to).

Undertiden skriver man cos²(v) i stedet for (cos(v))². Der er udelukkende tale om notation. Det betyder stadig cos(v)*cos(v). Med den nye notation bliver grundrelationen

$$\cos^2(v)+\sin^2(v)=1$$

Hvorfor er sammenhængen sådan?

Når vi skal forstå, hvordan grundrelationen er opstået, må vi se på, hvordan cosinus og sinus er defineret. Det er de ud fra enhedscirklen.

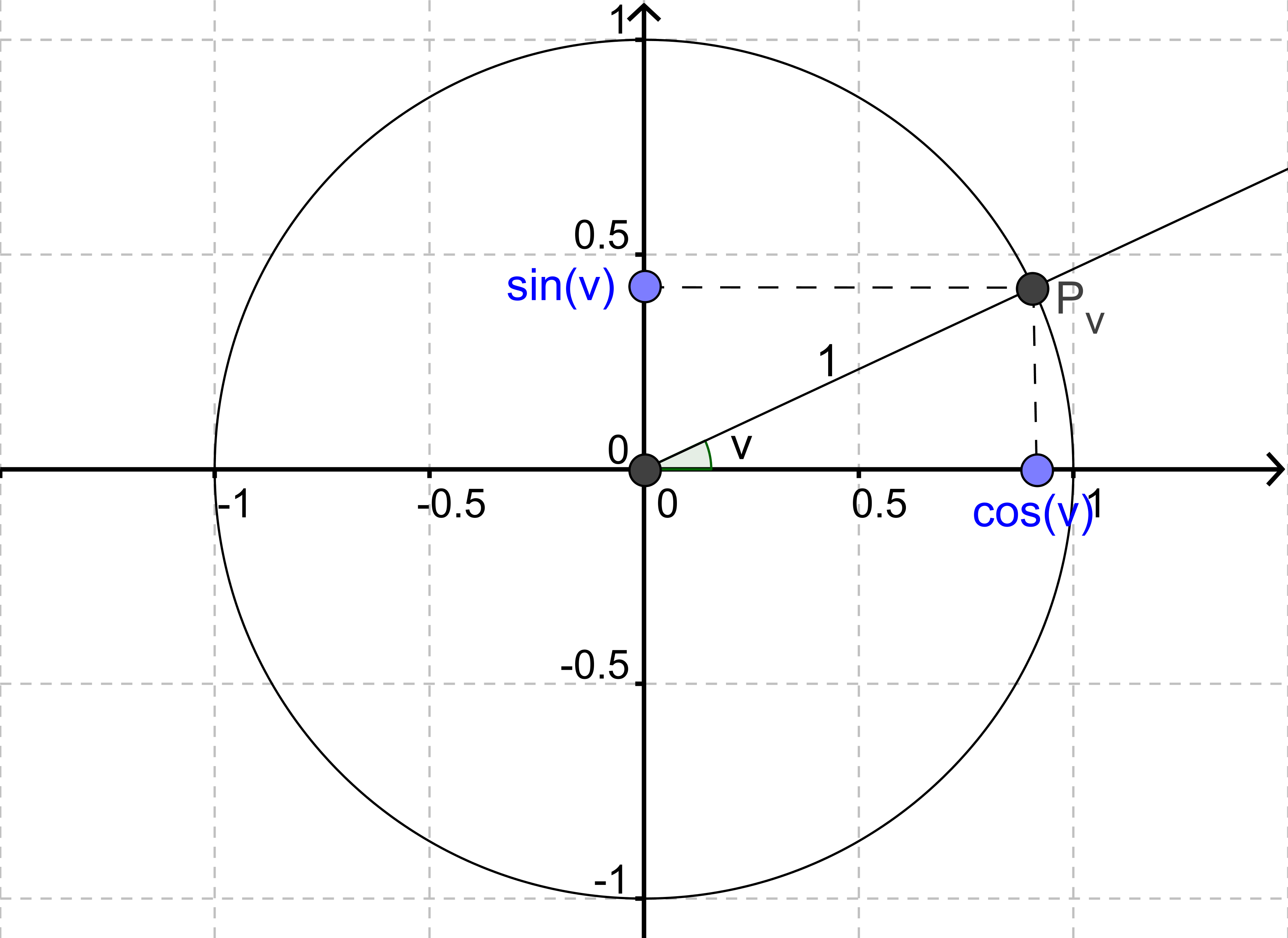
Punkterne origo, P_v og (cos(v), 0) danner en retvinklet trekant. Derfor kan vi bruge Pythagoras' læresætning. Vi ser, at den vandrette katete har længden cos(v), mens den lodrette har længden sin(v). Hypotenusen er radius i enhedscirklen og har derfor længden 1 pr. definition.

$$(1.\text{kat})^2+(2.\text{kat})^2=\text{hyp}^2$$

$$(\cos(v))^2+(\sin(v))^2=1^2\\\\(\cos(v))^2+(\sin(v))^2=1$$

Grundrelationen kaldes undertiden for "idiotreglen".

---

Videolektion