Toppunktsformlen

Toppunktet for et andengradspolynomium er det punkt, hvor parablen (andengradspolynomiets graf) har sit maksimum eller minimum.

Hvis der er tale om en glad parabel, så vil toppunktet være minimum for grafen

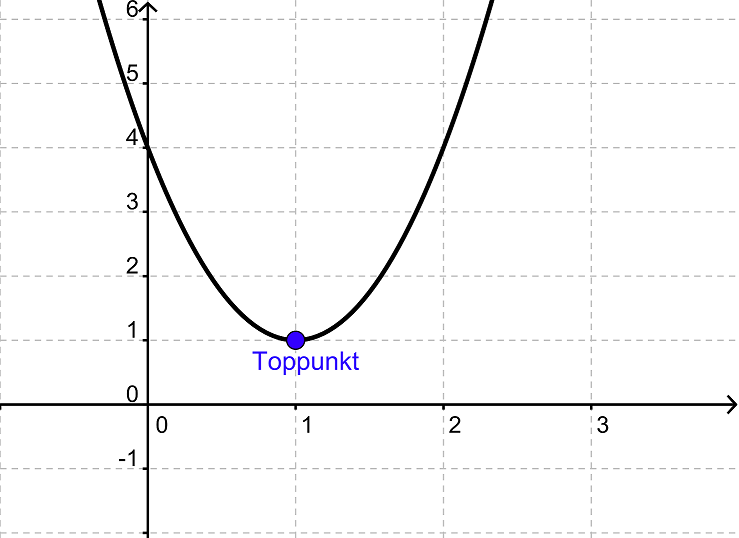
og hvis der er tale om en sur parabel, så vil toppunktet være maksimum for grafen.

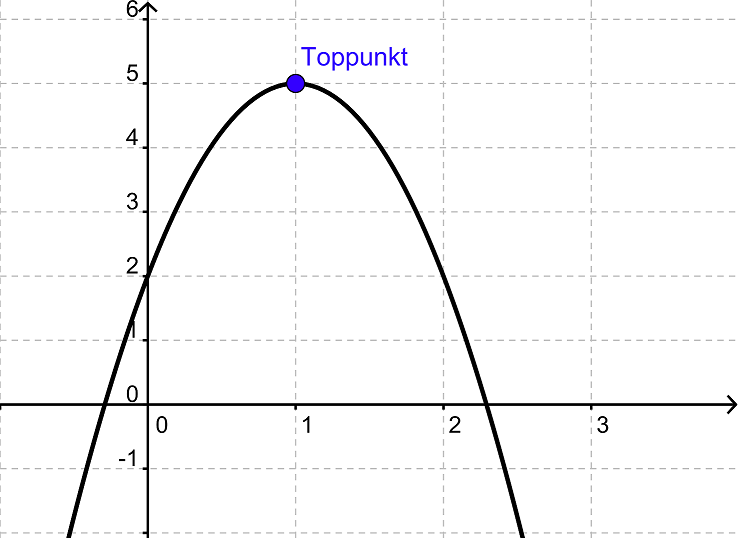
Der findes en formel for, hvordan man regner toppunktet ud. x-koordinaten, der under tiden betegnes T_x, udregnes således:

$$T_x=\frac{-b}{2a}$$

og y-koordinaten, der betegnes T_y, udregnes således:

$$T_y=\frac{-d}{4a}$$

Toppunktet er altså punktet:

$$(T_x,\:T_y)=\left (\frac{-b}{2a},\:\frac{-d}{4a} \right )$$

Lad os tage et eksempel.

Vi ønsker at finde toppunktet for andengradspolynomiet

$$f(x)=-3x^2+6x+2$$

Først udregner vi diskriminanten

$$d=b^2-4ac=6^2-4\cdot(-3)\cdot2=36+24=60$$

Nu er vi klar til at bestemme toppunktet

$$T_x=\frac{-b}{2a}=\frac{-6}{2\cdot(-3)}=\frac{-6}{-6}=1$$

$$T_y=\frac{-d}{4a}=\frac{-60}{4\cdot(-3)}=\frac{-60}{-12}=5$$

$$(T_x,\:T_y)=(1,\:5)$$

---

Videolektion