Vektorer
I dette afsnit kommer vi ind på det grundlæggende vektorbegreb.
En vektor er en pil, der har en længde og en retning. Man betegner oftest vektorer med små bogstaver med en lille pil over.
$$\overrightarrow{a}$$
En vektor har to koordinater, der beskriver hvor lang vektoren er i hhv. x-aksens og y-aksens retning. Man skriver koordinaterne i en søjle med x-koordinaten øverst og y-koordinaten nederst.
$$\overrightarrow{a}=\begin{pmatrix}a_1\\a_2\end{pmatrix}$$
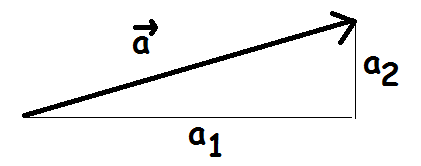
Når man tegner en vektor ind i et koordinatsystem, er det lige meget, hvor man starter. Så længe pilen har samme længde og retning, er det den samme vektor.

Her er eksempler på nogle vektorer med koordinater angivet

Ensrettede og modsatrettede vektorer
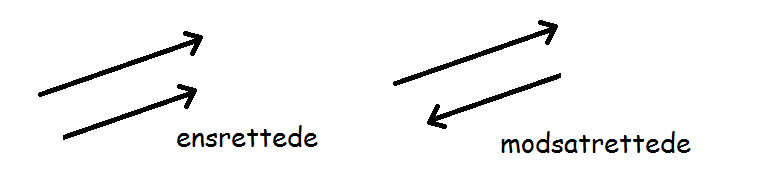
To vektorer, der er parallelle og har samme retning, kaldes ensrettede, mens to parallelle vektorer med hver sin retning kaldes modsatrettede.
Nulvektoren og egentlige vektorer
Den vektor, der har koordinaterne (0, 0) kaldes for nulvektoren
$$\overrightarrow{0}=\begin{pmatrix}0\\0\end{pmatrix}$$
Nulvektoren har samme start- og slutpunkt. Den har derfor ingen længde.
Alle vektorer, der ikke er nulvektoren, kaldes for egentlige vektorer.
Stedvektor
Hvis man er givet et punkt i planen, kan man tegne en vektor fra origo (punktet (0, 0)) hen til punktet. Denne vektor kaldes punktets stedvektor. Den betegnes med
$$\overrightarrow{OA}$$
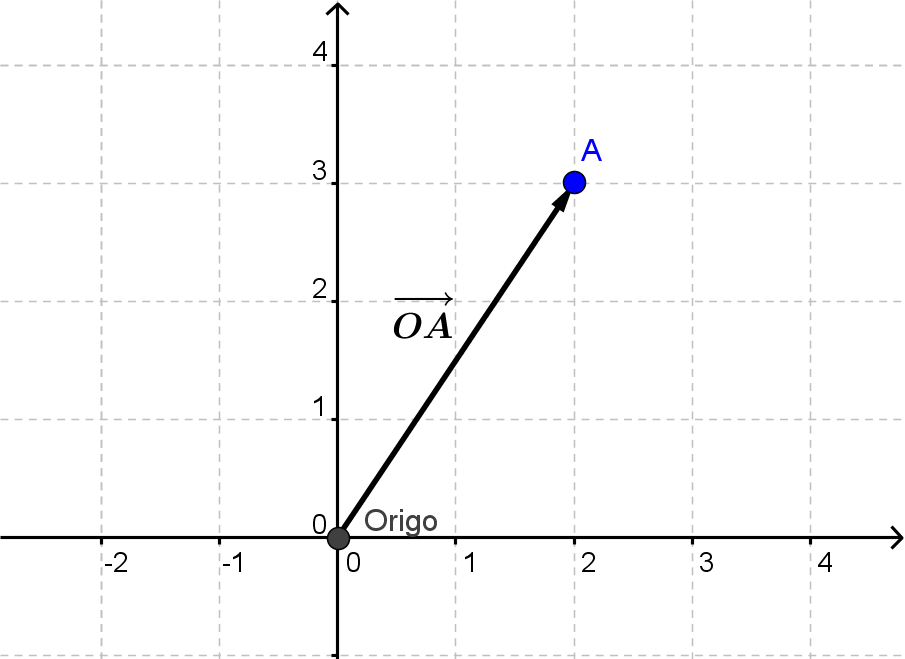
Stedvektoren til et punkt har samme koordinater som punktets koordinater.
$$A=(a_1,a_2)\quad\Leftrightarrow \quad\overrightarrow{OA}=\begin{pmatrix}a_1\\a_2\end{pmatrix}\\$$
Tværvektor
Hvis man har en vektor, kan man danne dens tværvektor. Tværvektoren har samme længde som den oprindelige vektor, men er drejet 90° mod urets retning. Tværvektoren betegnes med at sætte en lille "hat" (dvs "^") ovenpå vektoren.

Tværvektorens koordinater fås ved at bytte om på den oprindelige vektors koordinater og sætte et minus foran første koordinaten.
$$\hat{\overrightarrow{a}}=\begin{pmatrix}-a_2\\a_1\end{pmatrix}$$
Tværvektoren til en vektor a kaldes tit for "a hat", og det at finde tværvektoren kaldes tit "at hatte a".
Vektor mellem to punkter
Hvis man har to punkter, kan man tegne en vektor mellem dem.
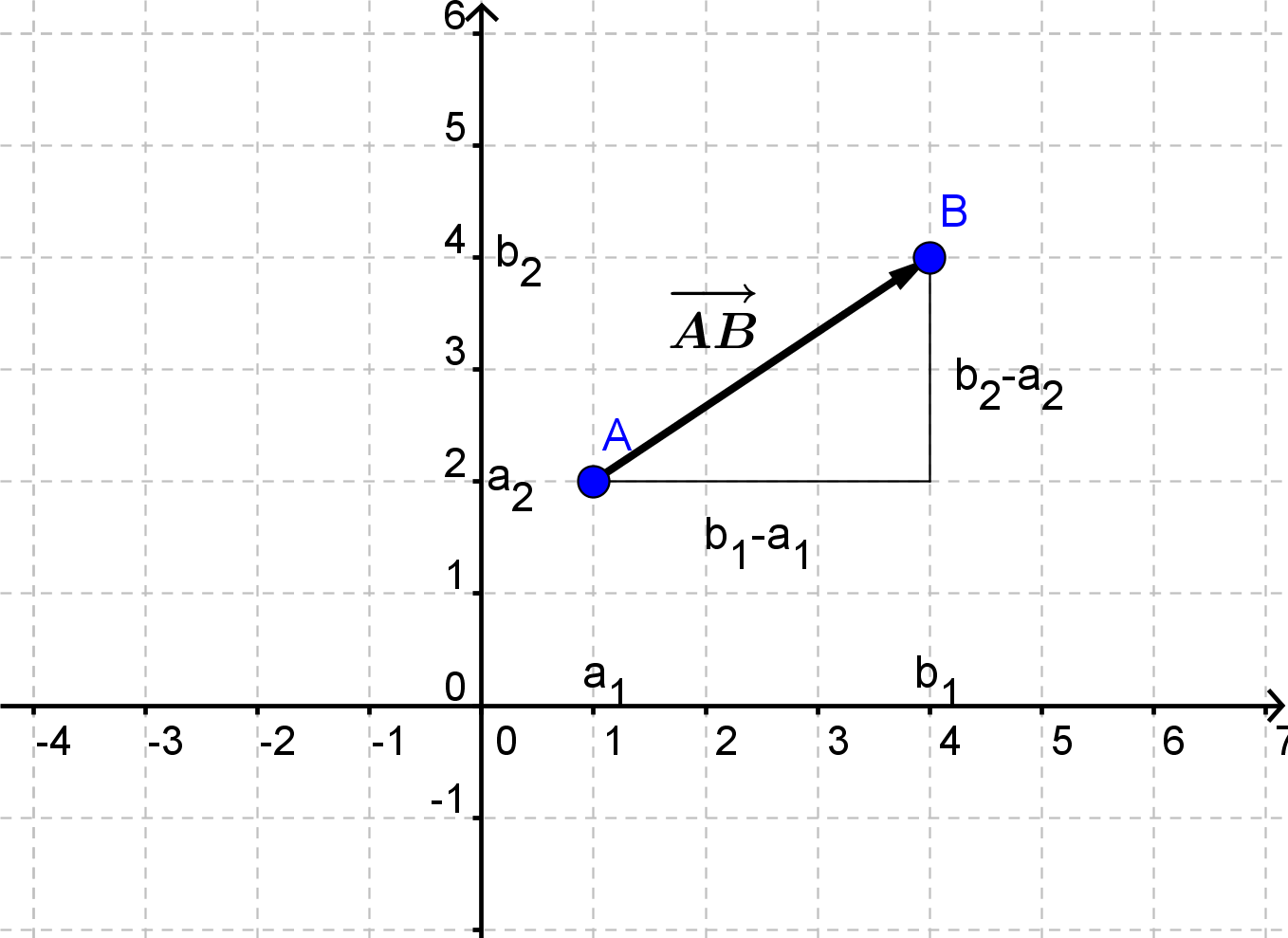
Vektoren vil have koordinaterne
$$\overrightarrow{AB}=\begin{pmatrix}b_1-a_1\\b_2-a_2\end{pmatrix}$$
Enhedsvektor
En enhedsvektor er en vektor, der har længde 1. F.eks vektoren
$$\overrightarrow{a}=\begin{pmatrix}1\\0\end{pmatrix}\\$$
For hver vinkel v, kan man danne enhedsvektoren
$$\begin{pmatrix} \cos(v)\\ \sin(v) \end{pmatrix}$$
der har længde 1 på grund af grundrelationen
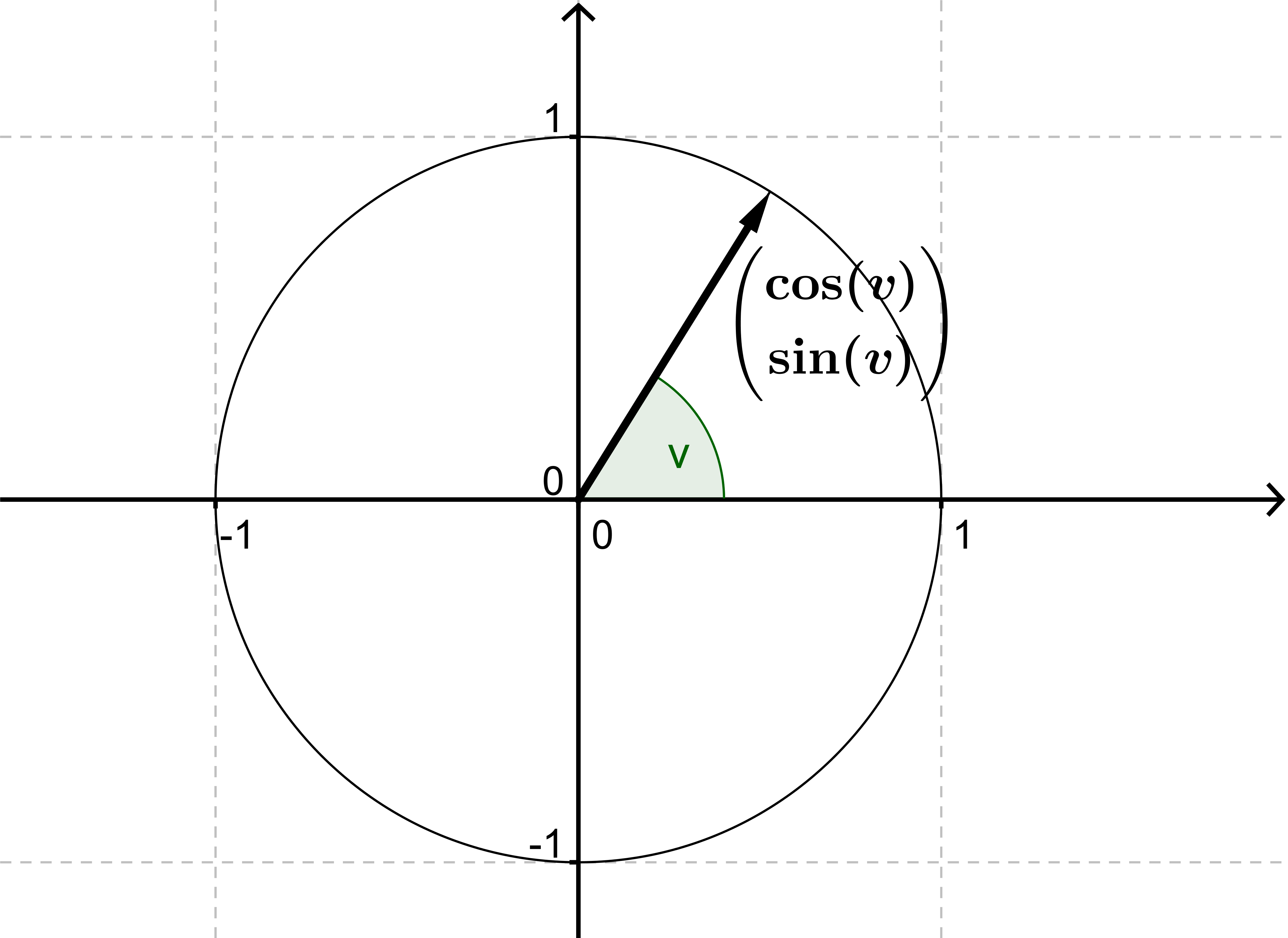
Hvis man har en vektor, a, kan man forkorte den, så man får en enhedsvektor, e, med samme retning ved hjælp af denne formel
$$\overrightarrow{e}=\frac{1}{|\overrightarrow{a}|}\overrightarrow{a}$$
