Tangentens ligning
Man kan bruge differentialregning til at bestemme en ligning for tangenten i et bestemt punkt på en funktion.
Hvis funktionen f er differentiabel i punktet (x0, f(x0)) - dvs. hvis der ikke er et knæk i det punkt - så er ligningen for tangenten i det punkt givet ved
$$y=f(x_0)+f'(x_0)\cdot(x-x_0)$$
Når vi bruger denne formel, skal vi sætte noget ind, der hvor der står x0, f(x0) og f '(x0). Men x og y skal vi lade være variable.
Hvorfor ser formlen sådan ud?
Fra teorien om rette linjer ved vi, at man finder hældningen til en ret
linje ved denne formel:
$$a=\frac{y_2-y_1}{x_2-x_1}$$
Hvis man i stedet for at have to faste punkter på grafen ( (x1, y1) og (x2, y2) ) har ét fast og ét løbende punkt (hhv. (x0, y0) og (x, y) ), kan man skrive den rette linjes ligning sådan her
$$a=\frac{y-y_0}{x-x_0}$$
Hvis vi ganger over med (x-x0) får vi
$$y-y_0=a\cdot(x-x_0)$$
Nu lægger vi y0 til på begge sider
$$y=y_0+a\cdot(x-x_0)$$
Det vi står med nu er altså ligningen til en ret linje, der går gennem det faste punkt (x0, y0). Vi ønsker at bestemme ligningen for tangenten i punktet (x0, f(x0)). Vores faste y-værdi er altså funktionsværdien til punktet x0. Derfor kan vi sætte y0=f(x0).
Vi ved fra teorien om differentialregning, at tangentens hældning i x0 er f '(x0). Derfor kan vi sætte a=f '(x0). Altså har vi nu
$$y=f(x_0)+f'(x_0)\cdot(x-x_0)$$
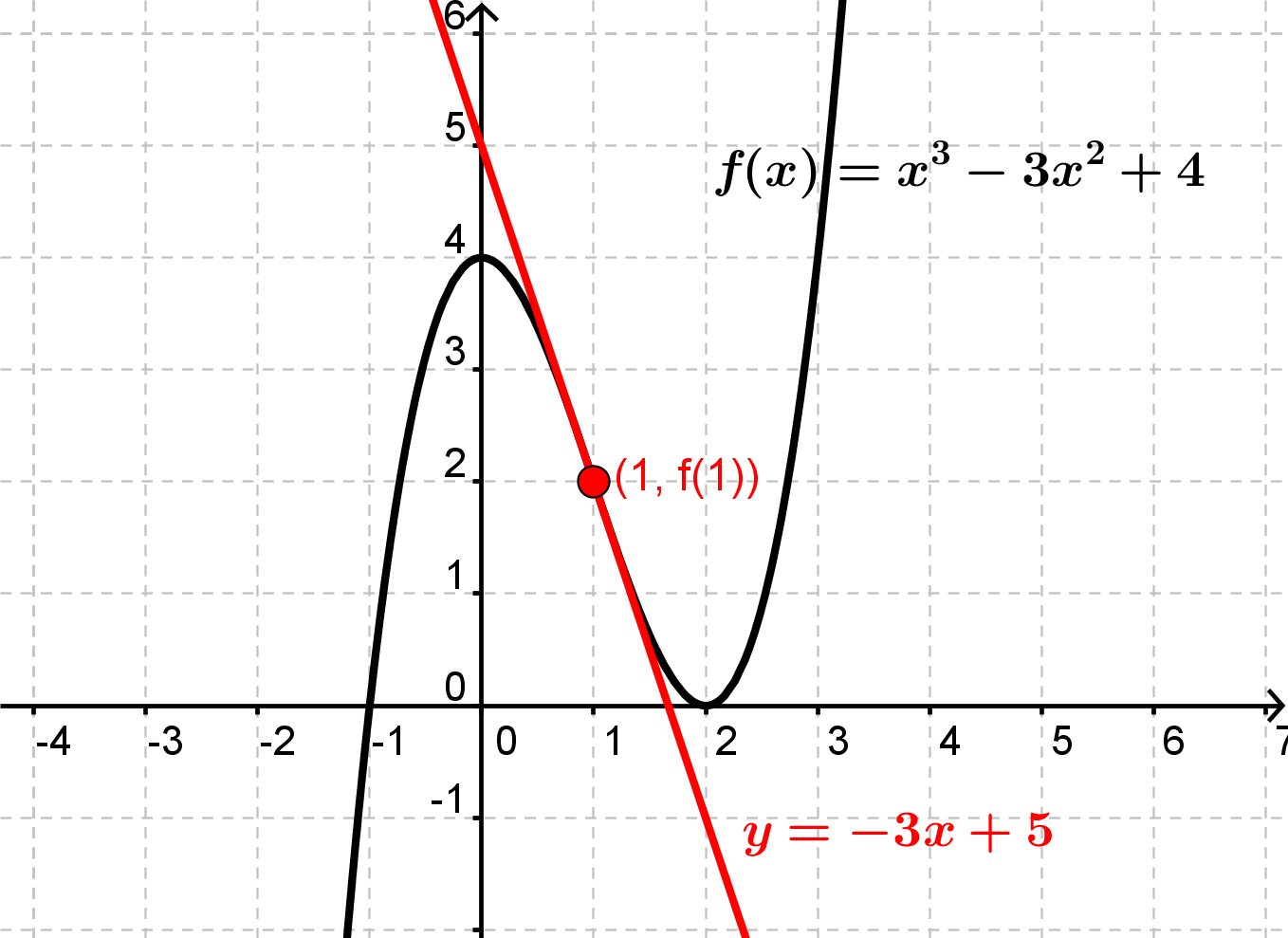
Eksempel
Vi har givet en funktion
$$f(x)=x^3-3x^2+4$$
og vi ønsker at finde dens tangent i punktet (1, f(1)).
Altså er
$$x_0=1$$
Så skal vi finde f(x0) ved at sætte x0 ind på x's plads i funktionsudtrykket.
$$f(1)=1^3-3\cdot1^2+4=1-3+4=2$$
Nu mangler vi bare at bestemme f '(x0). Det gør vi ved først at differentiere f og derefter at sætte x0 ind.
$$f'(x)=3x^{3-1}-3\cdot2x^{2-1}+0=3x^2-6x$$
$$f'(1)=3\cdot1^2-6\cdot1=3-6=-3$$
Nu kan vi sætte x0, f(x0) og f '(x0) ind i formlen for tangentens ligning.
$$y=f(x_0)+f'(x_0)\cdot(x-x_0)$$
$$y=2+(-3)\cdot(x-1)$$
$$y=2-3\cdot(x-1)$$
$$y=2-3x+3$$
$$y=-3x+5$$
Og så er vi færdige.