Linjens parameterfremstilling
I stedet for at beskrive en linje ved hjælp af en ligning, kan man gøre det ved hjælp af en parameterfremstilling. I en parameterfremtilling indfører man en parameter, der typisk kaldes t, og så ser man, hvordan et punkt (x, y) bevæger sig som funktion af t.
Linjens parameterfremstilling ser sådan her ud: Et punkt (x, y) ligger på linjen, når
$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}x_0\\y_0\end{pmatrix}+t\begin{pmatrix}r_1\\r_2\end{pmatrix}$$
Her er (x0,y0) et punkt på linjen, og vektor r er en retningsvektor for linjen.
Parameterfremstillingen fungerer på den måde, at man starter i sit faste punkt, og så går man en eller anden forlængelse (eller forkortelse) af retningsvektoren ud. På den måde, kan man ramme alle punkter på linjen. Det er størrelsen af t, der afgør, hvor meget man forlænger/forkorter retningsvektoren.
Nedenfor er tegnet et eksempel, hvor man sætter t=3 og t=-2.
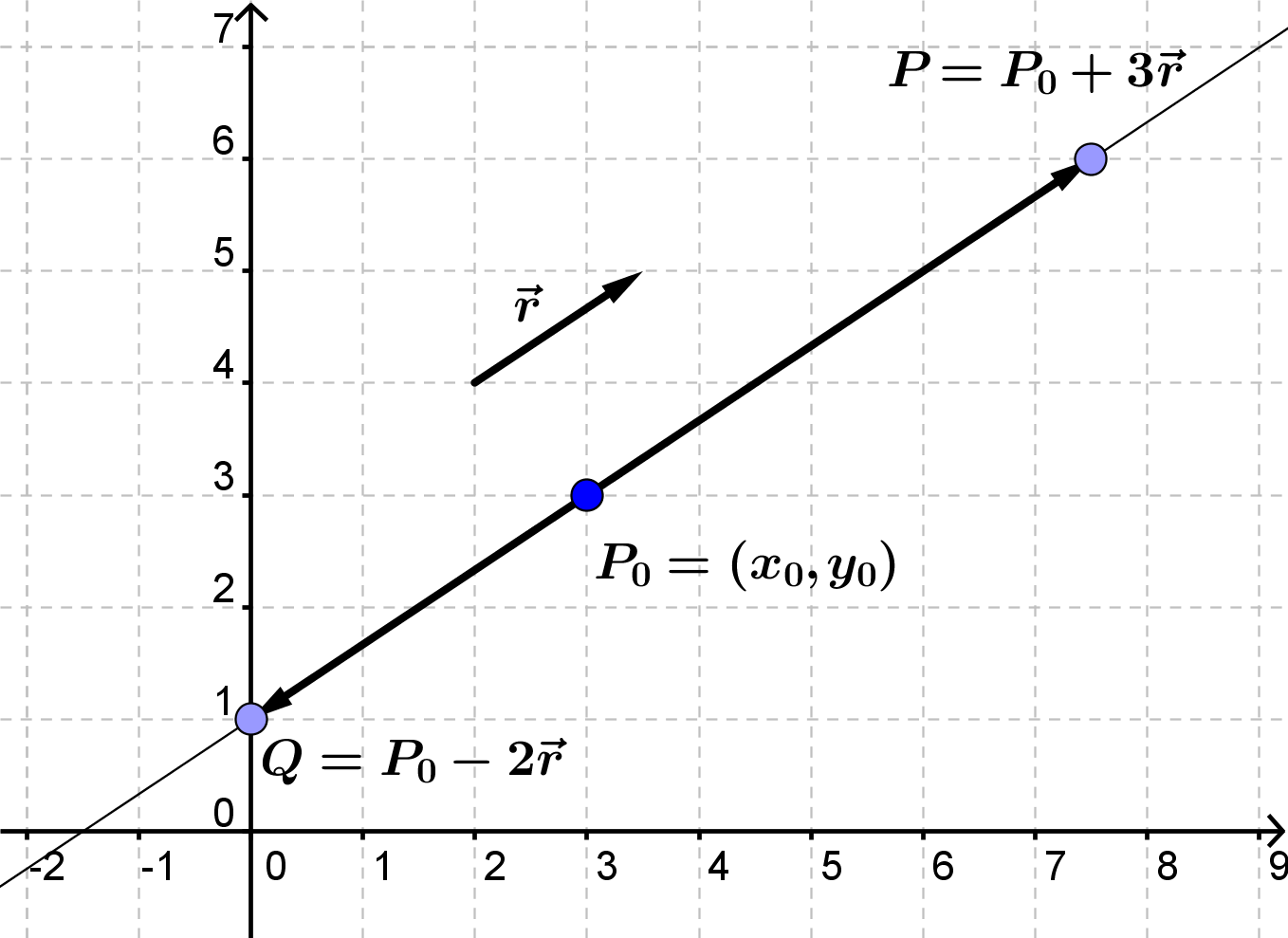
I stedet for at opskrive en parameterfremstilling som en ligning med vektorer, kan man opskrive forskrifter for hvert koordinat som funktion af t.
$$x(t)=x_0+t\cdot r_1$$
$$y(t)=y_0+t\cdot r_2$$
Kender punkt og retning
Hvis man kender et punkt på linjen og en retningsvektor, så kan man opskrive parameterfremstilling ved simpelthen at sætte ind i formlen ovenfor.
Hvis
$$P_0=(1,4)\text{ og }\overrightarrow{r}=\begin{pmatrix}2\\3\end{pmatrix}$$
så er parameterfremstillingen
$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\4\end{pmatrix}+t\begin{pmatrix}2\\3\end{pmatrix}$$
Eller hvis man skriver det som koordinatfunktioner
$$x(t)=1+2t$$
$$y(t)=4+3t$$
Kender to punkter
Hvis man kender to punkter på linjen, kan man opskrive parameterfremstillingen ved først at finde vektoren mellem punkterne. Denne må have samme retning som linjen. Dernæst kan man bruge et af punkterne som sit faste punkt, og vupti, så har man en parameterfremstilling.
Hvis vi kender
$$A=(1, 2)\text{ og }B=(4,3)$$
så kan vi finde
$$\overrightarrow{r}=\overrightarrow{AB}=\begin{pmatrix}4-1\\3-2\end{pmatrix}=\begin{pmatrix}3\\1\end{pmatrix}$$
og så skal vi bare vælge os et fast punkt. Det kunne f.eks. være A (men B havde virket lige så godt!).
$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}1\\2\end{pmatrix}+t\begin{pmatrix}3\\1\end{pmatrix}$$
Kender linjens ligning
Hvis man kender en ligning for linjen, kan man også omskrive til en parameterfremstilling.
I linjens ligning kan man aflæse en normalvektor. Denne står vinkelret på
linjen. Hvis man hatter normalvektoren får man en vektor, der er parallel med linjen. Den kan man bruge som retningsvektor.
Man kan finde et punkt på linjen ved at sætte en bestemt værdi ind på den ene variables plads og så isolere den anden.
Vores linje har ligningen
$$2x+5y+1=0$$
Vi aflæser en normalvektor til linjen til at være:
$$\overrightarrow{n}=\begin{pmatrix}2\\5\end{pmatrix}$$
Så må retningsvektoren være:
$$\overrightarrow{r}=\hat{\overrightarrow{n}}=\begin{pmatrix}-5\\2\end{pmatrix}$$
Nu skal vi finde et punkt på linjen. Vi sætter x=0 og ser hvilken y-værdi der passer til (vi kunne have sat x lig med hvad som helst, men det er tit lettere at regne på udtryk, hvor 0 indgår)
$$2\cdot0+5y+1=0$$
$$5y=-1$$
$$y=\frac{-1}{5}=-0,2$$
Så vores punkt er (0, -0,2)
Parameterfremstillingen er altså
$$\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}0\\-0,2\end{pmatrix}+t\begin{pmatrix}-5\\2\end{pmatrix}$$
eller skrevet som koordinatfunktioner
$$x(t)=-5t$$
$$y(t)=-0,2+2t$$
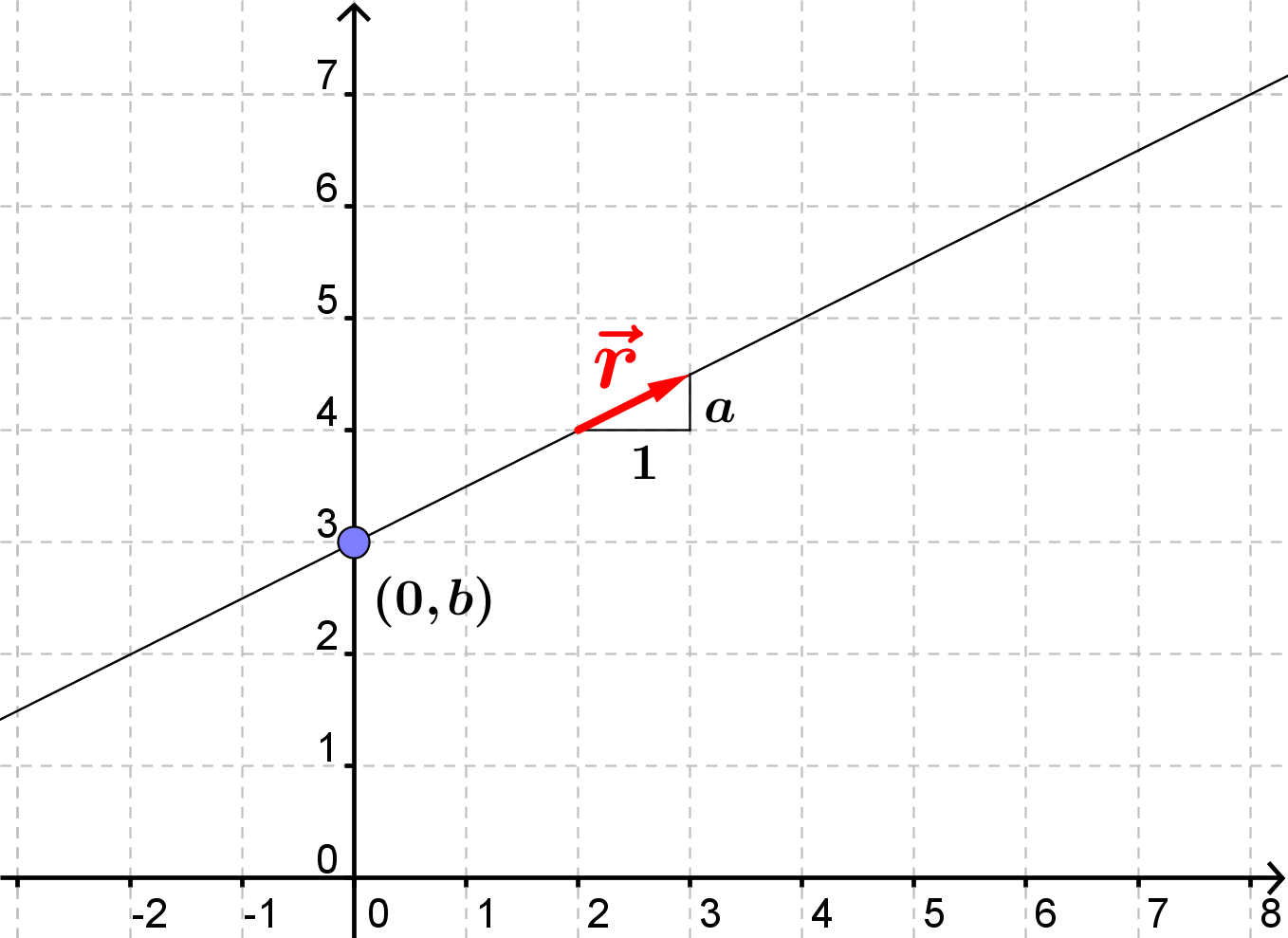
Hvis man i stedet havde kendt ligningen på formen y=ax+b, havde det været lettere. Der kunne vi som fast punkt bruge (0, b) og som retningsvektor bruge
$$\overrightarrow{r}=\begin{pmatrix}1\\a\end{pmatrix}$$