Sumkurver, kvartilsæt og boksplots

Hvis man har lavet en statistisk undersøgelse over folks højde, kunne man være interesseret i at finde ud af, hvor mange procent, der er under 175 cm, hvor mange procent der er mellem 172 og 182 cm høje, hvor høje de 25% mindste er osv. osv.

Spørgsmål af denne type kan let besvares ved hjælp af en sumkurve.

I en sumkurve har man sine observationer hen ad x-aksen og de kumulerede frekvenser op ad y-aksen.

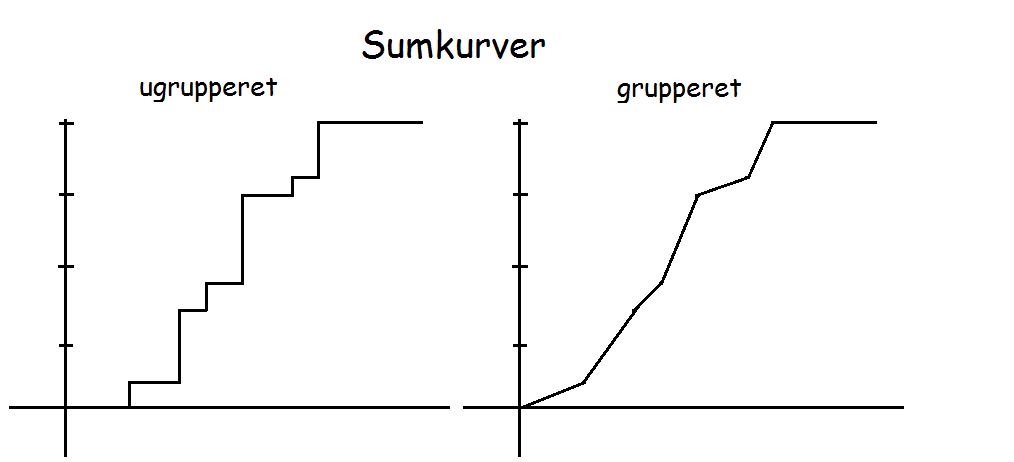
Ugrupperede vs. grupperede

Hvis ens data er ugrupperet, tegner man sin sumkurve ved fra sin observation at gå lodret op til den kumulerede frekvens. Derefter går man vandret hen til næste observation, hvorefter man går lodret op til dennes kumulerede frekvens. Man vil altså få en trappelignende figur.

Hvis ens data derimod er grupperet, tegner man sin sumkurve ved fra højre endepunkt af intervallet at afsætte den kumulerede frekvens. Når man har gjort det for alle intervallerne, forbinder man alle punkterne med rette linjer.

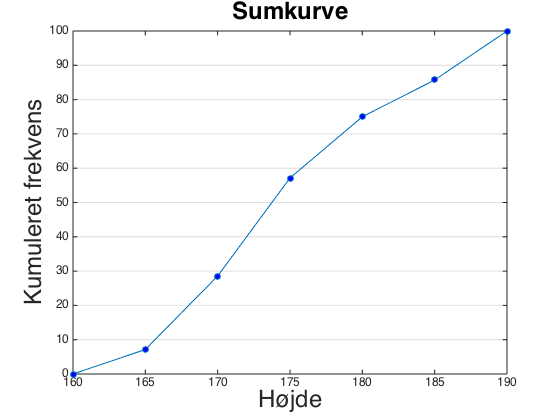
Lad os tegne en sumkurve ud fra et konkret datasæt og se, hvad man kan bruge den til.

Vores data er over højde

observation	hyppighed	frekvens	Kum.frekvens
]160;165]	2	7,14	7,14
]165;170]	6	21,43	28,57
]170;175]	8	28,57	57,14
]175;180]	5	17,86	75
]180;185]	3	10,71	85,71
]185;190]	4	14,29	100

Vi afsætter punkterne med højre endepunkt af intervallet på x-aksen og den kumulerede frekvens på y-aksen. Derefter forbinder vi dem, og får sumkurven:

Kvartilsæt

Kvartilsættet består af tre tal: øvre kvartil, median og nedre kvartil.
Medianen (Med) er det midterste tal af alle observationerne. 50% af observationerne er altså mindre end medianen og 50% er større.

Nedre kvartil (Q₁) er det tal, som 25% af observationerne er mindre end (og 75% større end).

Øvre kvartil (Q₃) er det tal, som 75% af observationerne er mindre end (og 25% større end).

Man aflæser sit kvartilsæt i sumkurven.

For at finde nedre kvartil, finder man 25% på y-aksen. Herfra går man vandret, til man støder på sumkurven. Nu går man lodret ned. Det tal, man støder på på x-aksen, er nedre kvartil.

På samme måde finder man medianen ved bare at gå ud fra 50%, og øvre kvartil ved at gå ud fra 75%.

For sumkurven ovenfor svarer det til

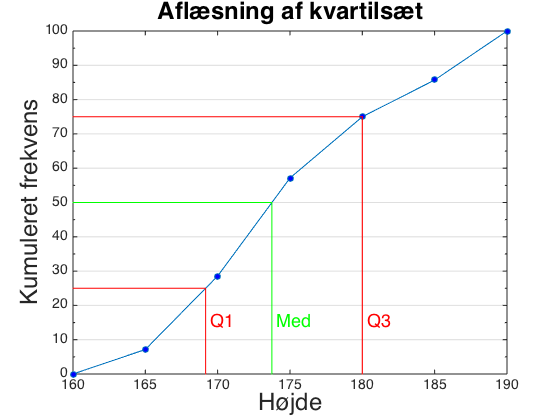
$$\text{Q}_1=169,\!2$$

$$\text{Med}=173,\!75$$

$$\text{Q}_3=180$$

Det vil altså sige, at :

• 25% af eleverne er 169,2 cm eller lavere.
• 50% af eleverne er 173,75 cm eller lavere
• 75% af eleverne er 180 cm eller lavere.

Hvis man vil finde ud af, hvor mange procent af eleverne, der er 172 cm eller lavere, så går man den anden vej end før. Man finder 172 på x-aksen, går lodret op til man rammer sumkurven og går derfra vandret ind til y-aksen.

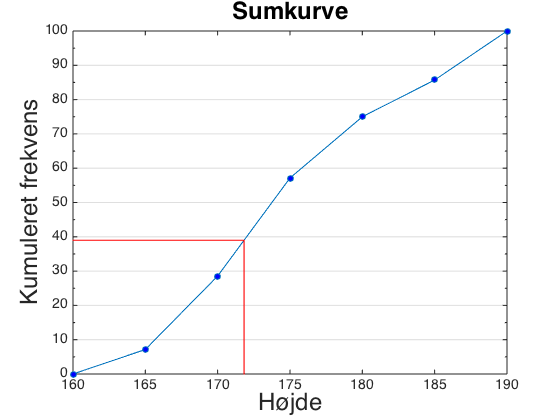
Vi kan altså aflæse, at 39% af eleverne er 172 cm eller lavere.

Hvor mange procent er mellem 172 cm og 182 cm høje?

I dette tilfælde aflæser man først, hvor mange procent, der er 182 cm eller lavere. Derfra trækker man, hvor mange procent, der er 172 cm eller lavere.

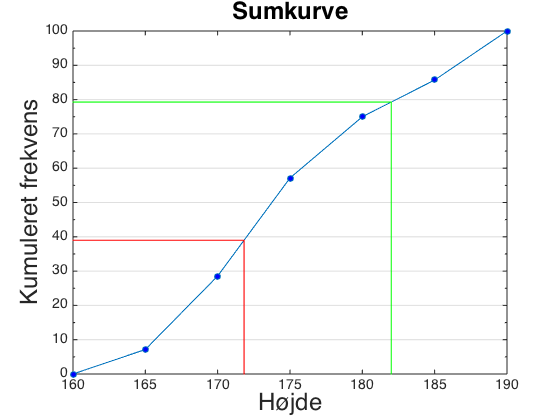
Vi kan aflæse, at 79% er 182 cm eller lavere.
Vi kan også aflæse, at 39% er 172 cm eller lavere.
Andelen, der er mellem 172 og 182 cm må derfor være 40% (=79%-39%)

Boksplot

Et boksplot er en overskuelig måde at fremstille sit data på.
For at kunne tegne et boksplot, skal man kende følgende værdier:

• mindste observation
• nedre kvartil
• median
• øvre kvartil
• største observation

Man har sine observationer hen ad x-aksen, og tegner sit boksplot på følgende måde:

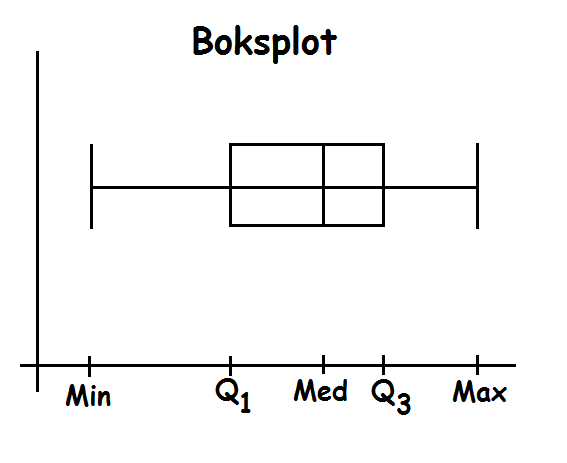
Bemærk, at det er ligegyldigt, hvor højt oppe, vi tegner vores boksplot. y-aksen har ingen betydning.

I et boksplot gælder altid, at:

• 25% af observationerne ligger mellem Min og Q_1.
• 25% af observationerne ligger mellem Q₁ og Med.
• 25% af observationerne ligger mellem Med og Q_3.
• 25% af observationerne ligger mellem Q₃ og Max.

Boksplots er gode til at sammenligne forskellige data med hinanden. Hvis to gymnasieklasser har taget den samme eksamen, kan man sammenligne deres resultater ved at tegne et boksplot for hver af dem.

---

Videolektion