Tangentligning til en cirkel
Hvis man kender en cirkel, kan det være nyttigt at finde en ligning for tangenten i et givet punkt, \(P_0\), på cirklen.
Tangenten er en ret linje, og man kan (som vi gennemgik i et tidligere afsnit) finde dens ligning ved at kende et punkt på linjen og en normalvektor.
Vi kender jo allerede et punkt på linjen, nemlig \(P_0\). Vi mangler altså bare en normalvektor. Heldigvis ved vi, at vektoren fra centrum til \(P_0\) står vinkelret på tangenten. Derfor kan vi bruge den som normalvektor.
Eksempel
Vores cirkel har ligningen
$$\mathcal{C}:\quad(x+2)^2+(y-1)^2=13$$
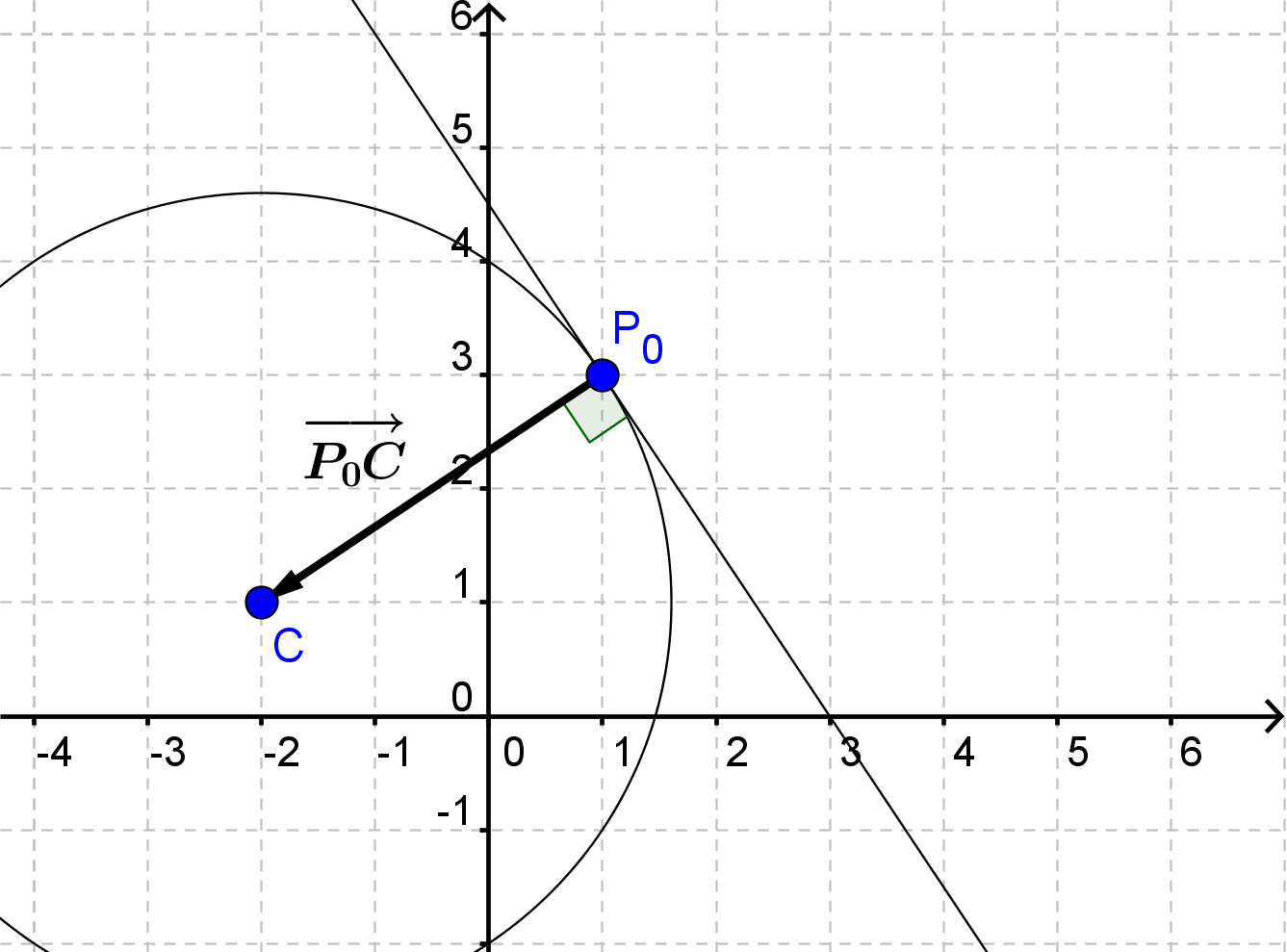
Punktet \(P_0=(1, 3)\) ligger på cirklen. Find en ligning for tangenten til cirklen i \(P_0\). Vi kan aflæse centrumkoordinaterne til \((-2, 1)\) (Vær opmærksom på fortegnene!). Nu finder vi vektoren mellem \( P_0 \) og \(C\)
$$\overrightarrow{n}=\overrightarrow{P_0C}=\begin{pmatrix}-2-1\\1-3\end{pmatrix}=\begin{pmatrix}-3\\-2\end{pmatrix}$$
Så sætter vi simpelthen bare ind i linjens ligning
$$
\begin{align}
0 & = a(x-x_0)+b(y-y_0) \Leftrightarrow\\
0 & = -3(x-1)-2(y-3) \Leftrightarrow\\
0 & = (-3x+3)+(-2y+6) \Leftrightarrow\\
0 & = -3x-2y+9
\end{align}
$$
og nu har vi en ligning for tangenten!