Sammenhæng mellem forskrift og graf
Ud fra et andengradspolynomiums forskrift kan man sige rigtig meget om grafens udseende. Det betyder, at man let kan danne sig et overblik over, hvordan grafen ser ud, uden, at man behøver tegne den.
Betydningen af a
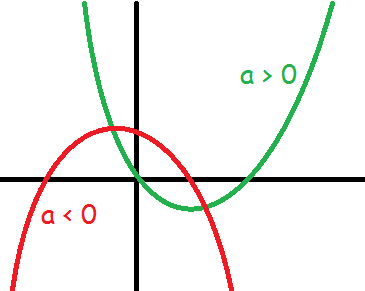
Fortegnet på tallet a afgør, om parablens grene peger opad eller nedad.
$$a>0\Leftrightarrow \text{parablens grene peger opad}$$
$$a<0\Leftrightarrow \text{parablens grene peger nedad}$$
Betydningen af b
Fortegnene af tallene a og b afgør, om toppunktet ligger til højre eller venstre for y-aksen.
$$a\:\text{og}\:b\:\text{samme fortegn}\Leftrightarrow \text{Toppunkt til venstre for y-aksen}$$
$$a\:\text{og}\:b\:\text{forskellige fortegn}\Leftrightarrow \text{Toppunkt til højre for y-aksen}$$
$$b=0\Leftrightarrow\text{Toppunkt på y-aksen}$$
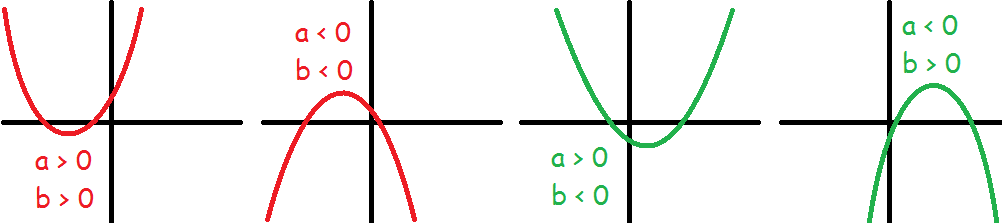
Betydning af c
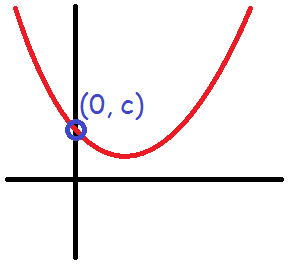
Tallet c afgør, hvor grafen skærer y-aksen. Dette sker i punktet (0, c).
Dette skyldes, at når vi sætter x=0 i forskriften for andengradspolynomiet, så får vi, at funktionsværdien er c.
$$f(0)=a\cdot0^2+b\cdot0+c=c$$
Betydningen af d
d, diskriminanten, udregnes som bekendt således:
$$d=b^2-4ac$$
Som vi husker fra afsnittet om diskriminantformlen, så afhænger
antallet af løsninger af fortegnet på d.
Vi husker også på, at løsningerne til en andengradsligning svarer til nulpunkterne for det tilsvarende andengradspolynomium.
Derfor siger diskriminanten noget om, hvor mange nulpunkter grafen har.
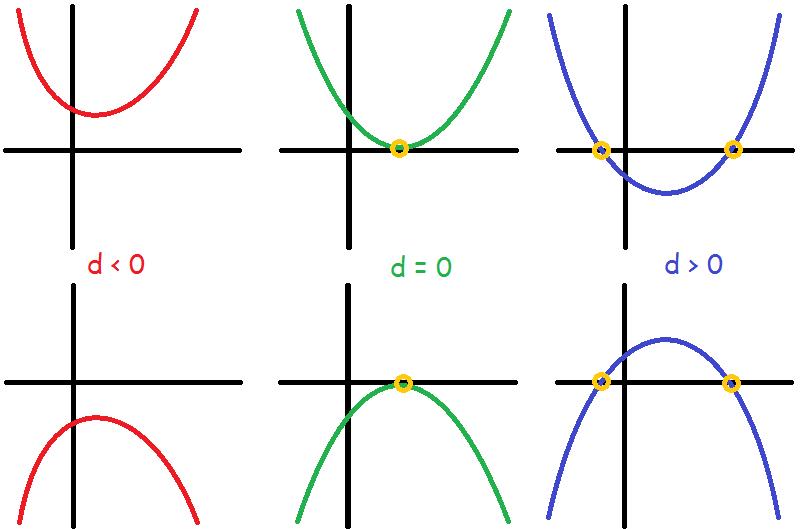
$$d<0\Leftrightarrow \text{ingen nulpunkter}\\d=0\Leftrightarrow 1\text{ nulpunkt}\\d>0\Leftrightarrow 2\:\text{ nulpunkter}$$
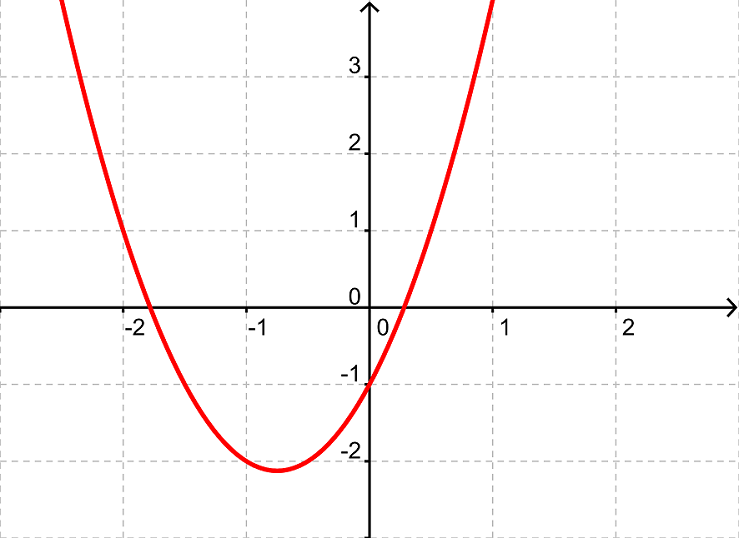
Eksempel:
$$f(x)=2x^2+3x-1$$
I denne andengradsligning er
a=2, b=3, c= -1 og
$$d=b^2-4ac=3^2-4\cdot2\cdot(-1)=9+8=17$$
Da a er positiv, er grafen en glad parabel
Da b også er positiv, befinder toppunktet sig til venstre for y-aksenDa c er -1, vil grafen skære y-aksen i punktet (0, -1)
Da d er positiv vil grafen have to nulpunkter.
Vi kan tegne grafen og tjekke, at vi har ret: