Differenskvotient og differentialkvotient
Når man differentierer en funktion, finder man tangenthældningen i et bestemt punkt. Den hældning, man finder, kaldes differentialkvotienten i punktet.
Men hvordan finder man tangenthældningen i ét punkt?
Vi ved fra c-niveau, hvordan man finder hældningen af en ret linje, hvis man kender to punkter på linjen. Det gør man ved at dividere ændringen af y-værdierne med ændringen af x-værdierne (læs mere her).
Vi starter på samme måde, når vi skal finde hældningen i ét punkt. Hvis vi ønsker at finde hældningen i punktet (x0, f(x0)), så starter vi med at gå et stykke, h, hen ad x-aksen og indtegner punktet (x0+h, f(x0+h)). Vi kan tegne sekanten, s, gennem de to punkter.
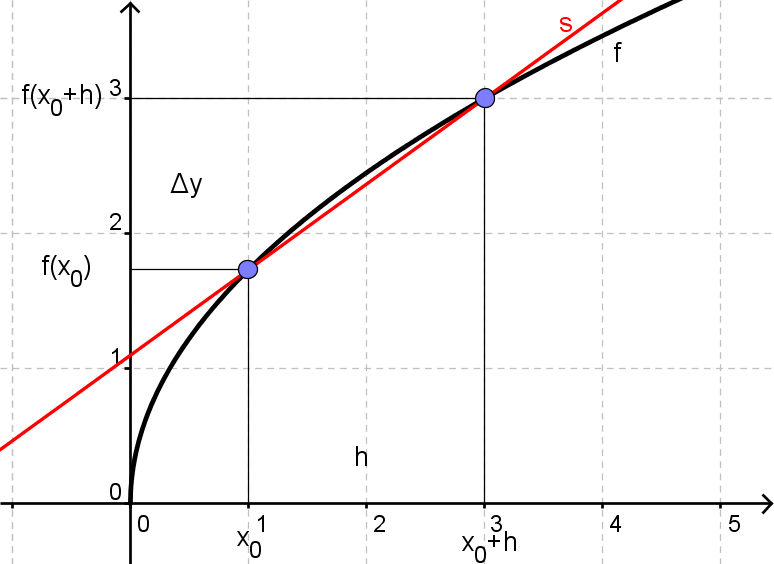
Vi kan beregne hældningen af sekanten som
$$a_s=\frac{y_2-y_1}{x_2-x_1}=\frac{f(x_0+h)-f(x_0)}{(x_0+h)-x_0}=\frac{f(x_0+h)-f(x_0)}{h}$$
Man kan også skrive det som
$$a_s=\frac{\Delta y}{h}=\frac{f(x_0+h)-f(x_0)}{h}$$
Man kalder sekanthældningen for differenskvotienten. Differenskvotienten er altså funktionstilvæksten divideret med h. Navnet kommer af, at der er tale om en kvotient (en brøk) hvor tælleren er differensen mellem funktionsværdierne.
Differentialkvotient
Hvis man nu gør h mindre, så nærmer hjælpepunktet sig vores faste punkt, og så vil sekanten komme til at ligne tangenten mere og mere.
Herunder er indtegnet tangenten (blå) og tre sekanter (røde) lavet ud fra forskellige h-værdier.
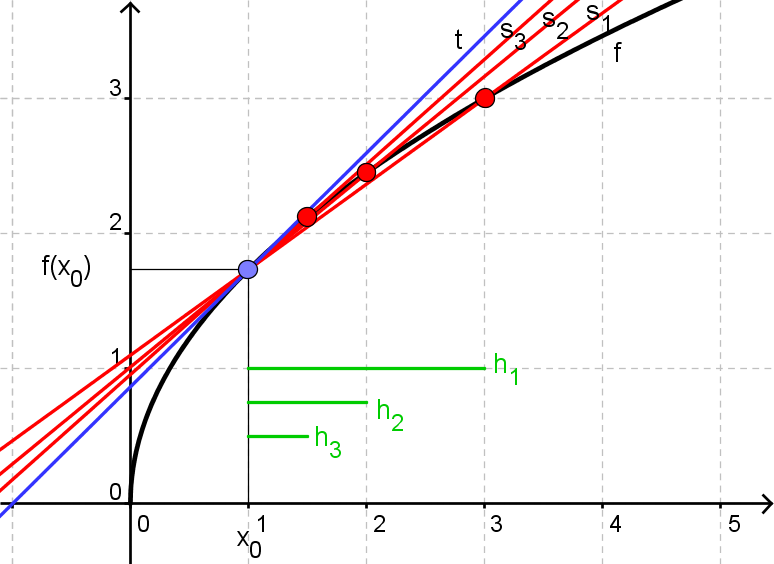
Hvis vi lader h blive uendelig lille, så vil sekanten nærme sig tangenten. Det er det, der er tricket i differentialregning!
Vi finder differenskvotienten og så ser vi, hvad der sker, når h bliver uendelig lille. Det resultat, vi får, kalder vi differentialkvotienten, og det svarer til tangentens hældning.
Man siger, at differentialkvotienten er grænseværdien af differenskvotienten for h gående mod 0.
$$a_t=\lim_{h\to0}(a_s)=\lim_{h\to0}(\frac{\Delta y}{h})$$
Man skriver også tit differentialkvotienten i x0 som
$$f'(x_0)$$
Dette læses "f mærke x0"
Eksempel
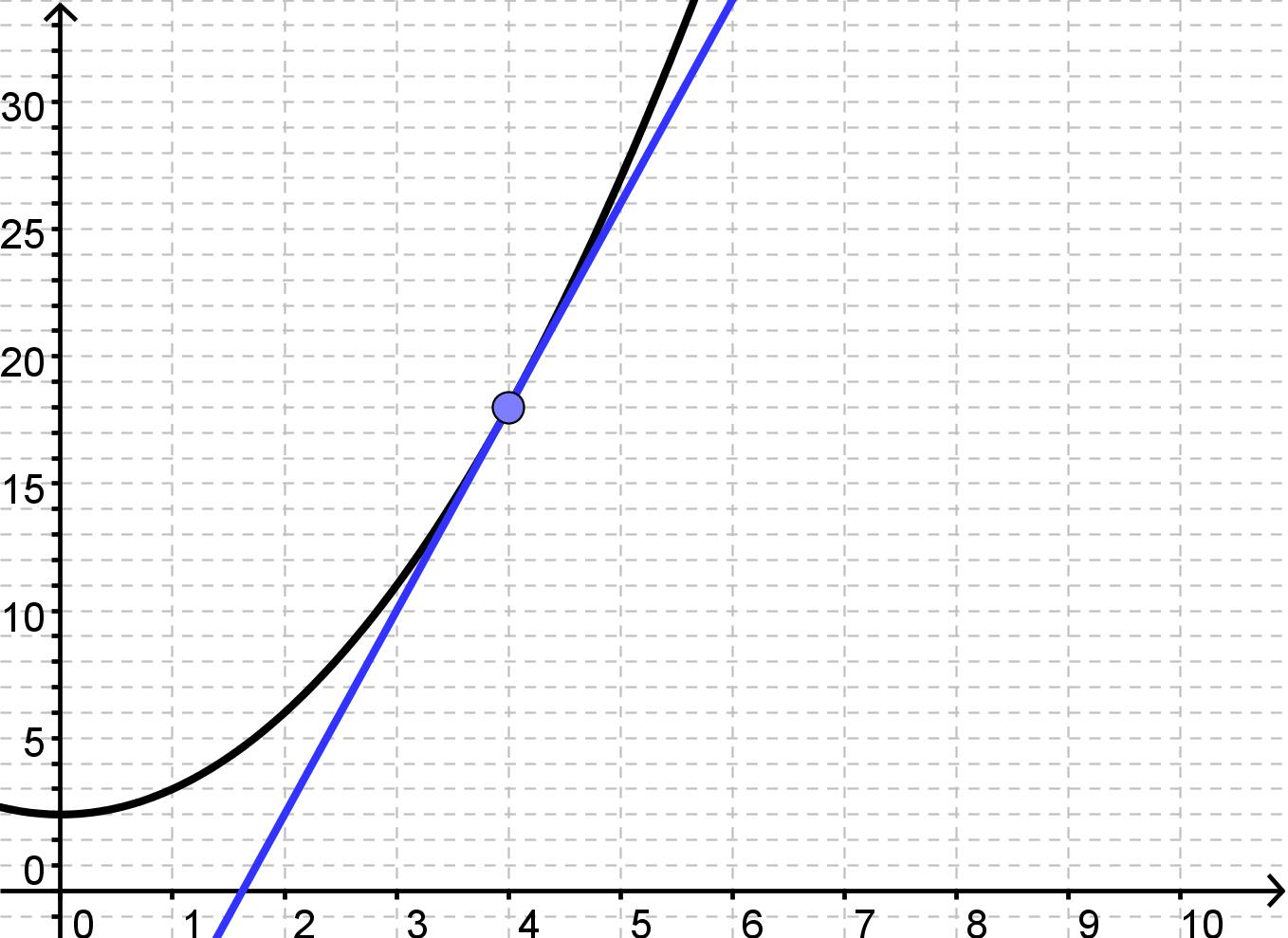
Vores funktion er f(x)=x2+3. Vi ønsker at finde differentialkvotienten når x0=4
Først finder vi funktionstilvæksten
$$f(4+h)=(4+h)^2+3=(\underbrace{16+h^2+8h}_{kvadratsætning})+3=h^2+8h+19$$
$$f(4)=4^2+3=16+3=19$$
$$\Delta y=f(4+h)-f(4)=(h^2+8h+19)-19=h^2+8h$$
Så finder vi differenskvotienten (dvs. sekanthældningen)
$$a_s=\frac{\Delta y}{h}=\frac{h^2+8h}{h}=\frac{h(h+8)}{h}=h+8$$
Så ser vi, hvad der sker, når h bliver uendeligt lille. Lige meget, hvor lille h bliver, så vil der ikke ske noget med 8-tallet. Men da h bliver meget lille vil det til sidst være så småt, at det er helt ubetydeligt.
$$a_t=\lim_{h\to0}(a_s)=\lim_{h\to0}(h+8)=8$$
Altså er differentialkvotienten
$$f'(4)=8$$
Det vil sige, at tangenten til f i punktet (4, f(4)) har en hældning på 8.