Normalfordeling

Når man laver statistiske eksperimenter, er det ofte man observerer, at data fordeler sig som en "klokkeform". Der er flest observationer inde mod midten, og så fordeler de sig ellers symmetrisk ud til begge sider.

Et eksempel kunne være disse data:

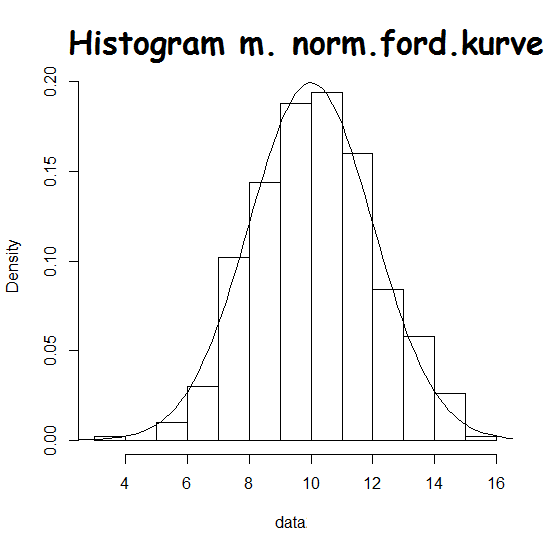
Her er tegnet et histogram over noget data (søjlerne) og derudover er indtegnet en normalfordelingskurve (klokkeformet kurve). Man kan se, at data fordeler sig næsten ligesom kurven.

Hvis man lavede intervallerne mindre (herover har de længde 1), ville søjlerne passe endnu bedre til klokkekurven.

Klokkeformen kan variere i både højde og bredde (afhængig af vores spredning). Men hvis bare data opfylder at være fordelt nogenlunde som en klokke, siger vi, det er normalfordelt.

Tjek om data er normalfordelt

Hvis man skal tjekke om noget data er normalfordelt, så er det smart først at tegne et histogram over det og se, om det danner noget, der minder om en klokkeform.

Hvis det er tilfældet, kan man indtegne det i et normalfordelingspapir. Her skal det danne en ret linje.

Man kan tegne bedste rette linje af punkterne i normalfordelingspapiret og direkte aflæse middelværdi og spredning

Hvad er der særligt ved normalfordelingen?

Hvis data er normalfordelt gælder der, at medianen (den midterste observation) er lig med middelværdien (gennemsnittet). Har man sumkurven for en normalfordeling, kan man altså aflæse middelværdien uden at lave nogen udregninger.

I en normalfordeling ligger data, så:

• 68,2 % ligger i intervallet [middelværdi - spredning ; middelværdi + spredning[
• 95,4 % ligger i intervallet [middelværdi - 2spredning ; middelværdi + 2spredning[
• 4,6 % ligger udenfor intervallet [middelværdi - 2spredning ; middelværdi + 2spredning[

På samme måde fordeler de sig på den anden side af middelværdien.

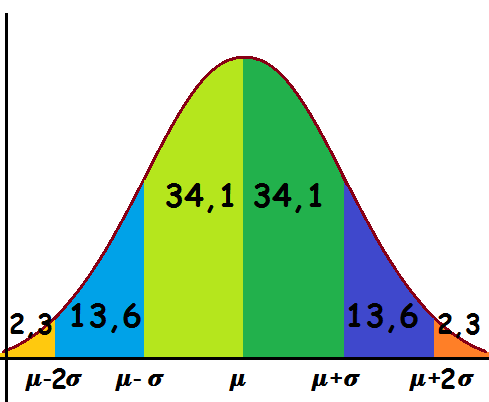
Der gælder desuden at normalfordelingens frekvensfunktion, φ, danner en klokkeformet graf og dens fordelingsfunktion, Φ, et symmetrisk S.

Frekvensfunktionen, som også er kaldet tæthedsfunktionen, er givet ved forskriften

$$φ(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$

hvor μ er middelværdien og σ er spredningen.

Man kan finde værdier af fordelingsfunktionen ved at integrere frekvensfunktionen.

Hvis vi har en normalfordeling med middelværdi 10 og spredning 1, er frekvensfunktionen

$$φ(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{(x-10)^2}{2}}$$

Hvis vi ønsker at se, hvor stor en del af vores observationer, der er 8,5 eller derunder, tager vi fordelingsfunktionens værdi i 8,5.

$$\phi(8,5)=\int_{-\infty}^{8,5}φ(x)\:dx=\int_{-\infty}^{8,5}\frac{1}{\sqrt{2\pi}}e^{-\frac{(x-10)^2}{2}}\:dx\approx0,0668=6,68\%$$

Integralet ovenfor kan ikke umiddelbart beregnes. Hvis man integrerer normalfordelingen får man et udtryk der indeholder en fejlfunktion, Erf(z). På engelsk hedder den errorfunction, heraf Erf. Fejlfunktionen er kort sagt sandsynligheden for, at ens observation ligger i det interval man undersøger i integralet.

Da Erf(z) ofte forekommer i statistikken og visse differentialligninger kan den slås op i mange CAS-værktøjer, Excel, lommeregnere og andet. 
Integralet kan bestemmes direkte ved brug af CAS-værktøjer (TI-Nspire, Maple), hvilket er den korrekte fremgangsmåde i gymnasiet.

Avanceret

Fejlfunktionen er ikke en simpel funktion og kan derfor ikke beregnes på en simpel måde. Den kan bestemmes ved bl.a. approksimation ved Taylorpolynomier, men det er ud over pensum i gymnasiet, og først noget man stifter bekendtskab med på universitetet.

Erf funktionen er defineret ved 

$$Erf(z) = \frac{2}{\sqrt{\pi}} \int_{-\infty}^z e^{-t^2} dt $$

Ved integration af normalfordelingen finder man

$$\int_{-\infty}^z \varphi(x) dx = \frac{1}{2} \sqrt{\sigma} (1+ Erf(\frac{z - \mu}{\sqrt{2 \sigma}})), \, \mathrm{forudsat} \, \sigma \geq 0$$

Taylor ekspansionen for Erf(z)

$$Erf(z) = \frac{2}{\sqrt{\pi}} \sum_{n=0}^{\infty} \frac{(-1)^n z^{2n+1}}{n!(2n+1)}$$ 

Hvor z er et komplekst tal.