Regression

I forrige afsnit har vi kun vist, at \(y = 2,5 \cdot x\) beskriver punkterne bedre end \(y = 1,5 \cdot x\). Vi har stadig ikke fundet den optimale funktion. Her skal vi bruge den viden vi har fra et andet område af matematikken, der også beskæftiger sig med funktioner: differentialregning.

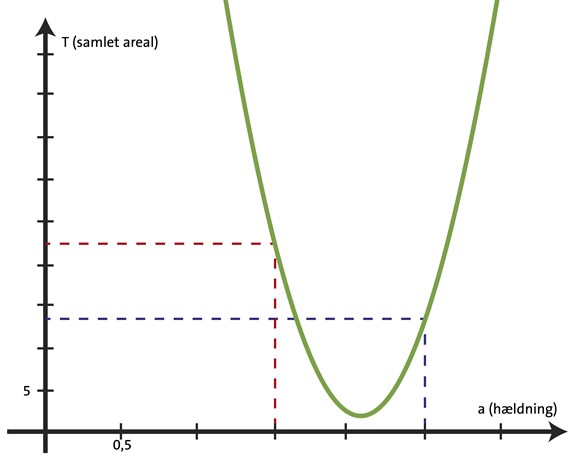
Hvis vi forestiller os kvadraternes samlede areal, \(T\), som en funktion af proportionalitetsfaktoren, \(a\), så vil den være et andengradspolynomium. Det kan vi vise med en udvidelse af kvadratreglen \((c - a \cdot b)^2 = c^2 + a^2 \cdot b^2 - 2abc\). Da \(a\) er den eneste ubekendte, så kan alle andre led reduceres til et enklte tal, og når den samlede sum findes vil den højeste eksponent \(a\) har stadig være \(2\).

En af fordelene ved et andengradspolynomium er, at det altid har et toppunkt som kan findes ved at sætte den afledte funktion lig nul. At toppunktet i vores model vil være det globale minimum skyldes, at alle koefficienterne for \(a^2\) er positive, da de er vores x-værdier kvadreret.

I eksemplet fra tidligere havde vi punkterne \(P\), \(Q\) og \(S\). Sætter vi dem ind i vores funktion for \(T(a)\) får vi:

\(T(a) = (2 - a \cdot 1)^2 + (7 - a \cdot 4)^2 + (15 - a \cdot 7)^2 = 66 \cdot a^2 - 270 \cdot a + 278\)
\(T'(a) = 66 \cdot 2 \cdot a - 270 = 132 \cdot a - 270\)

Hvis vi så sætter T’(a) lig nul får vi toppunktets førstekoordinat, der er:

\(132 \cdot a - 270 = 0\)
\(a = \frac{270}{132} \approx 2,045\)

Den bedst beskrivende proportionalitetsfaktor er altså cirka 2,045. Og det samlede areal er:

\(T( \frac{270}{132} ) = \frac{41}{22} \approx 1,86\)

Den samme procedure kan overføres til eksponentialfunktioner af typen \(a^x\) og potensfunktioner \(x^a\). Det næste logiske skridt ville være at tilføje en ekstra variabel til de tre tilfælde, dette overlader vi dog til et CAS-program.