Cirkler og linjers skæring
Når man har med cirkler og linjer at gøre, kan det ofte være nyttigt at finde ud af, om de skærer hinanden, og hvad koordinatsættene til skæringspunkterne i så fald er.
Der er 3 muligheder for antal skæringer, når man ser på cirkler og linjer. Hvis linjen skærer cirklen er der to skæringspunkter, hvis linjen tangerer cirklen er der ét røringspunkt, og hvis cirklen og linjen slet ikke krydser hinanden er der (selvfølgelig) ingen skæringspunkter.
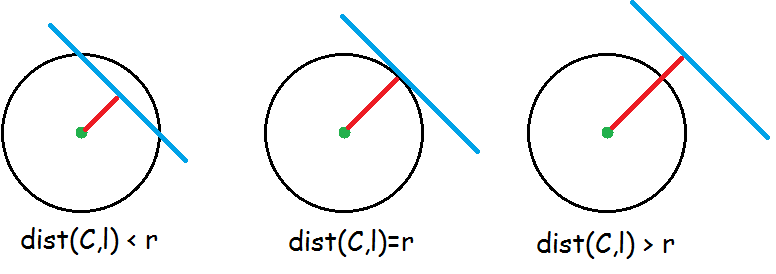
Hvis man kender cirklens centrumkoordinater og linjens ligning, kan man beregne den vinkelrette afstand mellem centrum og linje ved hjælp af distanceformlen. Hvis denne afstand er mindre end radius vil der være to skæringer, hvis den er lig radius vil der være et røringspunkt, og hvis den er større end radius vil der ikke være nogen skæringer.
Eksempel:
Skærer linjen l: y=2x+4 cirklen C: (x-1)2+(y+3)2=36 ?
Cirklens centrum er altså (1, -3) og radius er 6.
Vi finder afstanden mellem linjen og cirklen vha. distanceformlen
$$\text{dist}(C,l)=\frac{|ax_1+b-y_1|}{\sqrt{a^2+1}}=\frac{|2\cdot1+4-(-3)|}{\sqrt{2^2+1}}=\frac{9} {\sqrt{5}}\approx4,02$$
Da afstanden mellem centrum og linje er mindre end radius er der altså to skæringer.
Bestemme koordinaterne for skæringspunkterne
Når man har bestemt antallet af skæringspunkter, kan man måske også være interesseret i at finde koordinaterne for disse skæringer.
Dette gør man ved at sætte de to ligninger sammen. Man sætter linjens ligning ind på y's plads i cirklens ligning. Derved får vi en andengradsligning med x som eneste ubekendte. Den løser vi, og vi har så x-koordinaterne for. Disse indsættes så i linjens ligning for at finde de tilsvarende y-koordinater.
Vi illustrerer det med et eksempel.
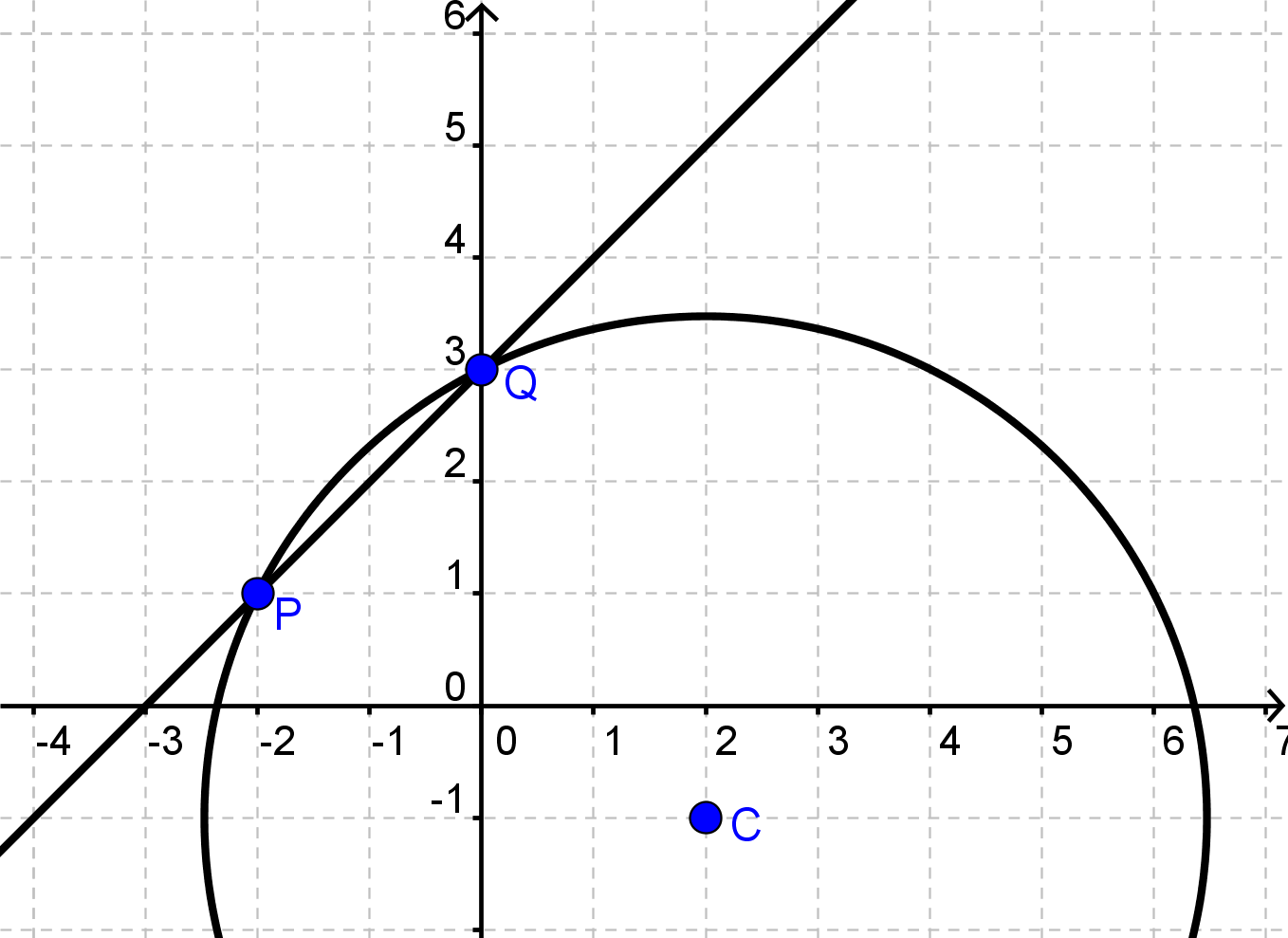
Lad cirklen være givet ved ligningen
$$(x-2)^2+(y+1)^2=20$$
og linjen ved ligningen
$$y=x+3$$
Man kan tjekke efter, at de har to skæringer. For at finde koordinaterne til skæringerne sættes udtrykket for y i linjens ligning ind i cirklens ligning.
$$(x-2)^2+({\color{Red} y}+1)^2=20$$
$$(x-2)^2+({\color{Red} {x+3}}+1)^2=20$$
$$(x-2)^2+(x+4)^2=20$$
Nu udregner vi parenteserne ved hjælp af kvadratsætningerne
$${\color{Red} {(x-2)^2}}+{\color{Blue} {(x+4)^2}}=20$$
$${\color{Red}{x^2+4-4x}}+{\color{Blue}{ x^2+16+8x}}=20$$
$$2x^2+4x+20=20$$
$$2x^2+4x=0$$
Vi har nu en andengradsligning, som vi løser ved hjælp af nulreglen
$$2x^2+4x=0$$
$$2x(x+2)=0$$
$$x=0\vee x=-2$$
Disse to x-værdier er x-koordinaterne for de to skæringspunkter. Ved at indsætte dem i linjens ligning, får vi de tilsvarende y-værdier.
$$y=x+3$$
$$y_1=0+3=3$$
$$y_2=-2+3=1$$
Skæringspunkterne er altså
$$(0,\:3)\quad \text{og}\quad(-2,\:1)$$