Funktionstilvækst
Som nævnt tidligere handler differentialregning om at finde ud af, hvor hurtigt funktioner vokser/aftager.
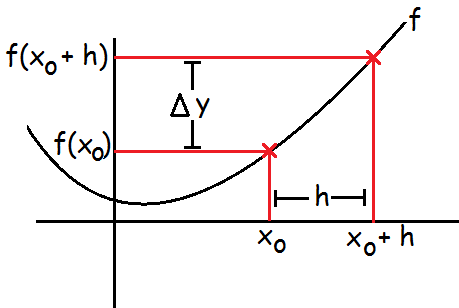
Derfor er man nødt til først at finde ud af, hvor meget funktionen vokser. Man bruger indenfor matematikken tit det græske bogstav Δ (delta) til at beskrive en tilvækst.
Hvis man har et fast punkt x0 og man ønsker at se, hvor meget funktionen ændres (vokser/aftager), hvis man går et lille stykke, h, hen på x-aksen, så kan man beregne funktionstilvæksten, Δy.
$$\Delta y=y_2-y_1=f(x_0+h)-f(x_0)$$
Lad os tage et eksempel. Vores funktion er f(x) = x2 - 2x, og det punkt, vi ønsker at bestemme funktionstilvæksten fra er x0 = 3
Vores formel for funktionstilvæksten er altså
$$\Delta y=f(3+h)-f(3)$$
Vi finder først f(3+h) ved at sætte 3+h ind på x's plads i funktionsudtrykket.
$$f(3+h)=(3+h)^2-2(3+h)=(3+h)^2-6-2h$$
Vi bruger kvadratsætningerne til at reducere udtrykket
$$(3+h)^2-6-2h=(9+h^2+6h)-6-2h=h^2+4h+3$$
Nu udregner vi f(3):
$$ f(3) = 3^2 -2\cdot 3 = 9-6=3 $$
Funktionstilvæksten er derfor
$$\Delta y=f(3+h)-f(3)=(h^2+4h+3)-(3)=h^2+4h$$
Afhængig af, hvor stor h er (hvor stort et skridt vi tager på x-aksen), kan vi altså bestemme, hvor stor funktionstilvæksten vil blive ved at sætte denne h-værdi ind.
Eksempel med tredjegradspolynomium
Vi kan også tage et eksempel med et tredjegradspolynomium. Vi betragter funktionen f(x)=x3+4x, og vælger nu vores begyndelsespunkt x0 til at være 2. Vi har igen, at:
$$ \Delta y = f(2+h) -f(2) $$
Vi finder f(2+h) på samme måde som før:
$$f(2+h) = (2+h)^3 + 4(2+h) = (2+h)^3 +8+4h$$
Denne gang skal vi bruge en kubiksætning på udtrykket, da det står i tredje potens:
$$(2+h)^3 +8+4h = 2^3 +h^3 +3 \cdot 2^2 h + 3\cdot 2 h^2 +8+4h \\ = 8 +h^3 +12 h + 6 h^2 +8+4h = h^3 +6h^2 + 16h +16 $$
Så udregner vi f(2):
$$f(2) = 2^3 +4 \cdot 2 = 8+8=16$$
Nu kan vi bestemme funktionstilvæksten:
$$ \Delta y = h^3 +6h^2 + 16h +16 - 16 =h^3 +6h^2 +16h $$
Det er altså samme princip for polynomier af højere orden, men vi får nogle noget mere besværlige udtryk at arbejde med.
