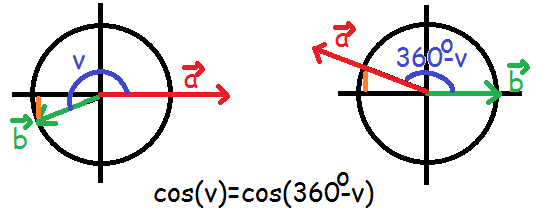Vinkel mellem vektorer
Hvis man tegner to (egentlige) vektorer ud fra samme begyndelsespunkt, vil der dannes en vinkel mellem dem. Man kan beregne denne vinkel vha. følgende formel
$$\cos(v)=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}|\cdot|\overrightarrow{b}|}\quad,\qquad\overrightarrow{a},\overrightarrow{b}\neq\overrightarrow{0}$$
cosinus til vinklen mellem to vektorer er altså skalarproduktet af divideret med produktet af deres længder.
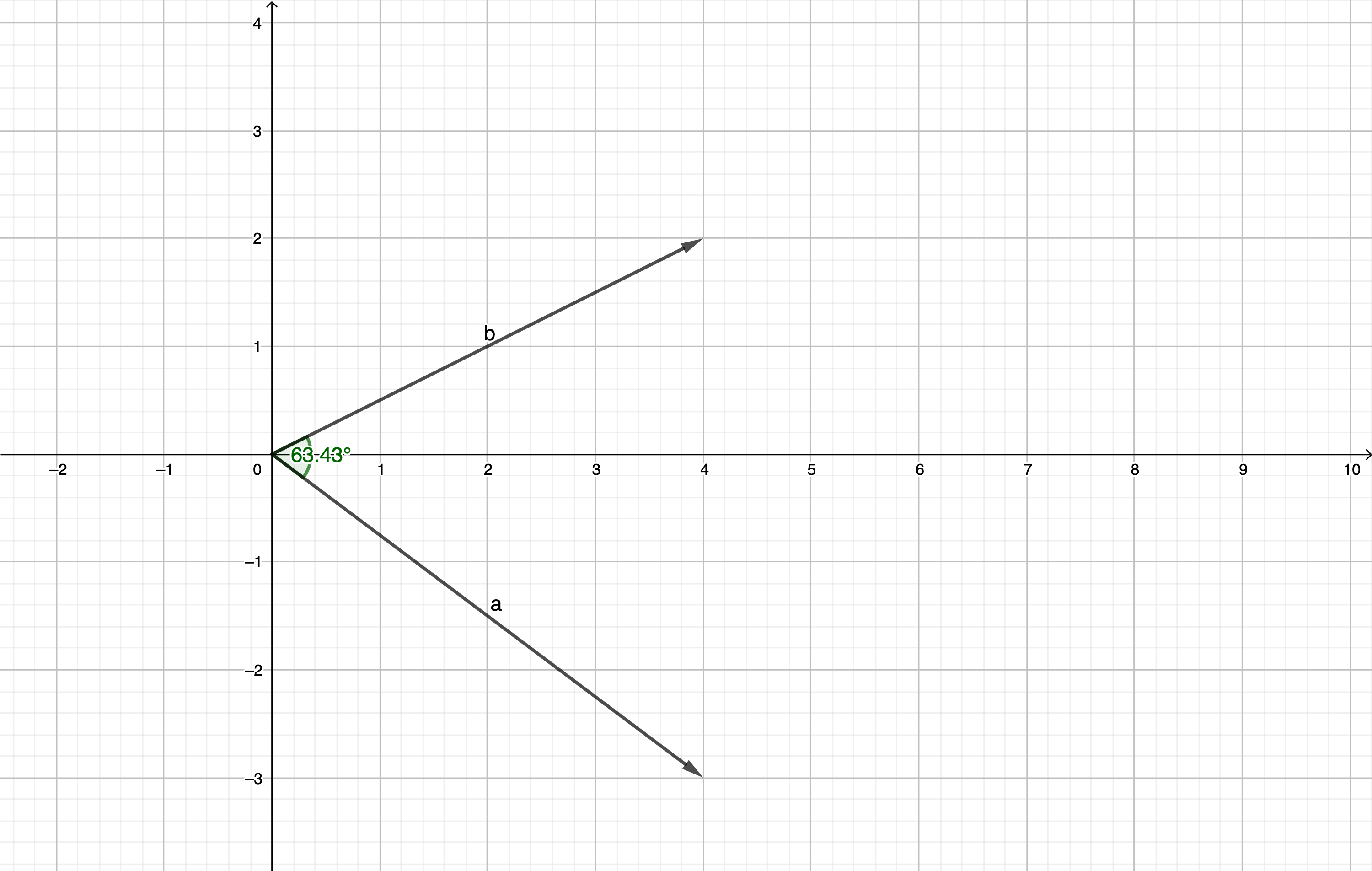
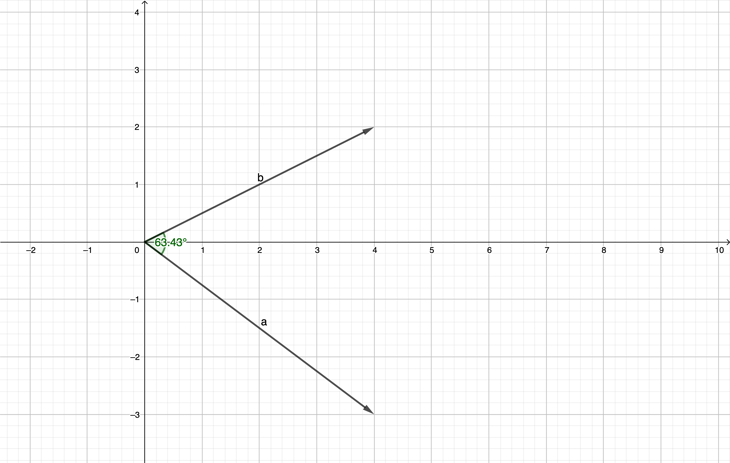
Hvis vi ønsker at finde vinklen mellem
$$\begin{pmatrix}4\\-3\end{pmatrix}\text{ og }\begin{pmatrix}4\\2\end{pmatrix}$$
kan vi beregne den således
$$\cos(v)=\frac{\begin{pmatrix}4\\-3\end{pmatrix}\cdot\begin{pmatrix}4\\2\end{pmatrix}}{\left|\begin{pmatrix}4\\-3\end{pmatrix}\right|\cdot\left|\begin{pmatrix}4\\2\end{pmatrix}\right|}=\frac{4\cdot4+(-3)\cdot2}{\sqrt{4^2+(-3)^2}\sqrt{4^2+2^2}}=\frac{16-6}{\sqrt{25}\sqrt{20}}\approx0,455$$
$$v=\cos^{-1}(0,4545)\approx62{,}96^\circ$$
Skalarprodukt og vinkel
I formlen for vinklen mellem to vektorer indgår et skalarprodukt. Lad os prøve at isolere det.
$$\cos(v)=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}|\cdot|\overrightarrow{b}|}$$
$$\overrightarrow{a}\cdot\overrightarrow{b}=\cos(v)\cdot|\overrightarrow{a}|\cdot|\overrightarrow{b}|$$
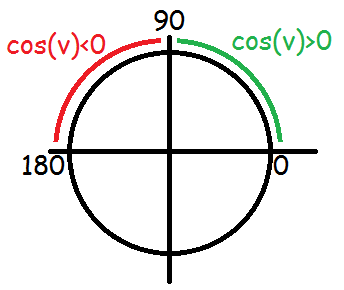
Hvis skalarproduktet (venstresiden) er positiv, så er højresiden også positiv. Da længderne af a og b altid er positive, betyder det at cos(v) er positiv. cos(v) er positiv, når v er under 90°.
Hvis skalarproduktet er negativt, så er højresiden også negativ. Men da længderne altid er positive, betyder det, at cos(v) er negativ. cos(v) er negativ når v ligger mellem 90 og 180°.
Hvis skalarproduktet er 0, så er højresiden 0. Det betyder at cos(v) er 0. Og det betyder at vinklen mellem vektorerne er 90°
Altså kan vi sige
$$\overrightarrow{a}\cdot\overrightarrow{b}>0\quad\Leftrightarrow \quad v\text{ er spids}$$
$$\overrightarrow{a}\cdot\overrightarrow{b}<0\quad\Leftrightarrow \quad v\text{ er stump}$$
$$\overrightarrow{a}\cdot\overrightarrow{b}=0\quad\Leftrightarrow \quad v\text{ er ret}$$
Hvad hvis vinklen mellem vektorerne er over 180º?
Hvis vinklen mellem vektor a og vektor b er over 180, så vil vinklen mellem vektor b og vektor a være mindre end 180. De to vinkler vil tilmed have samme cosinus-værdi, så det er ikke noget, man behøver tænke over i udregningerne. Når man taler om vinklen mellem to vektorer, vil man typisk tale om den under 180.