Regning med vektorer
Ligesom med tal, kan man lægge vektorer sammen og trække dem fra hinanden. Man kan ikke gange vektorer med hinanden, men der findes noget der minder om, som vi kommer tilbage til senere. Man kan forlænge eller forkorte en vektor ved at gange den med et tal. Der findes ingen måder, hvorpå man kan dividere vektorer med hinanden!
Først vil vi definere, hvordan man addererer og subtraherer vektorer med hinanden, samt hvordan man ganger en vektor med et tal. Bagefter vil vi komme ind på, hvilke regneregler, der gælder for disse regneoperationer.
Man lægger to vektorer sammen ved at lægge dem sammen koordinatvist. Man lægger altså førstekoordinaterne sammen og bagefter lægger man andenkoordinaterne sammen
$$\overrightarrow{a}+\overrightarrow{b}=\begin{pmatrix}a_1+b_1\\a_2+b_2\end{pmatrix}\\$$
Hvis man skal tegne en vektorsum, svarer det til først at tegne den ene vektor og i forlængelse af den tegne den den anden vektor. Når man forbinder den førstes startpunkt og den andens slutpunkt, får man vektorsummen.
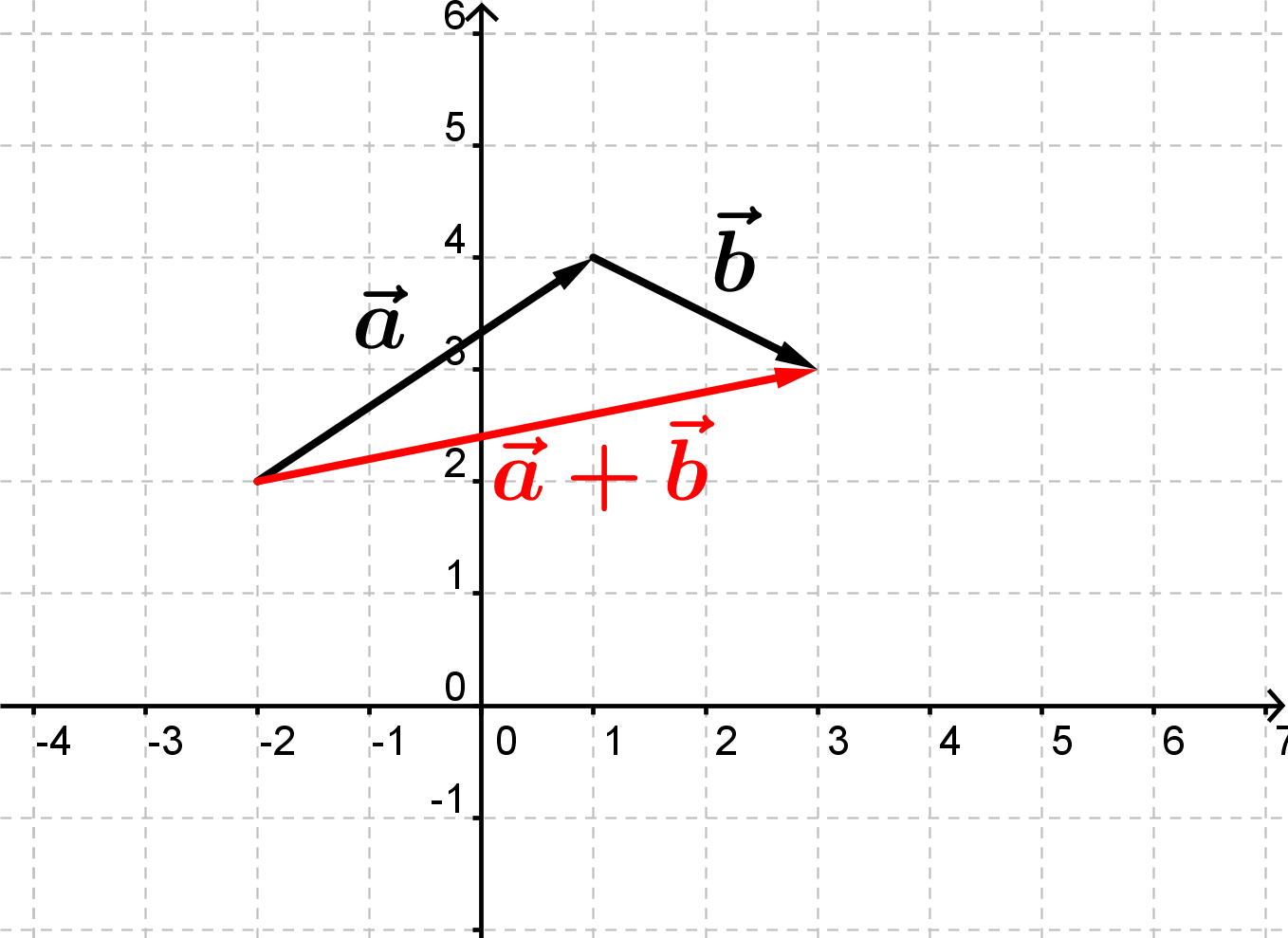
Når man trækker vektorer fra hinanden, gør man det ligeledes koordinatvist.
$$\overrightarrow{a}-\overrightarrow{b}=\begin{pmatrix}a_1-b_1\\a_2-b_2\end{pmatrix}$$
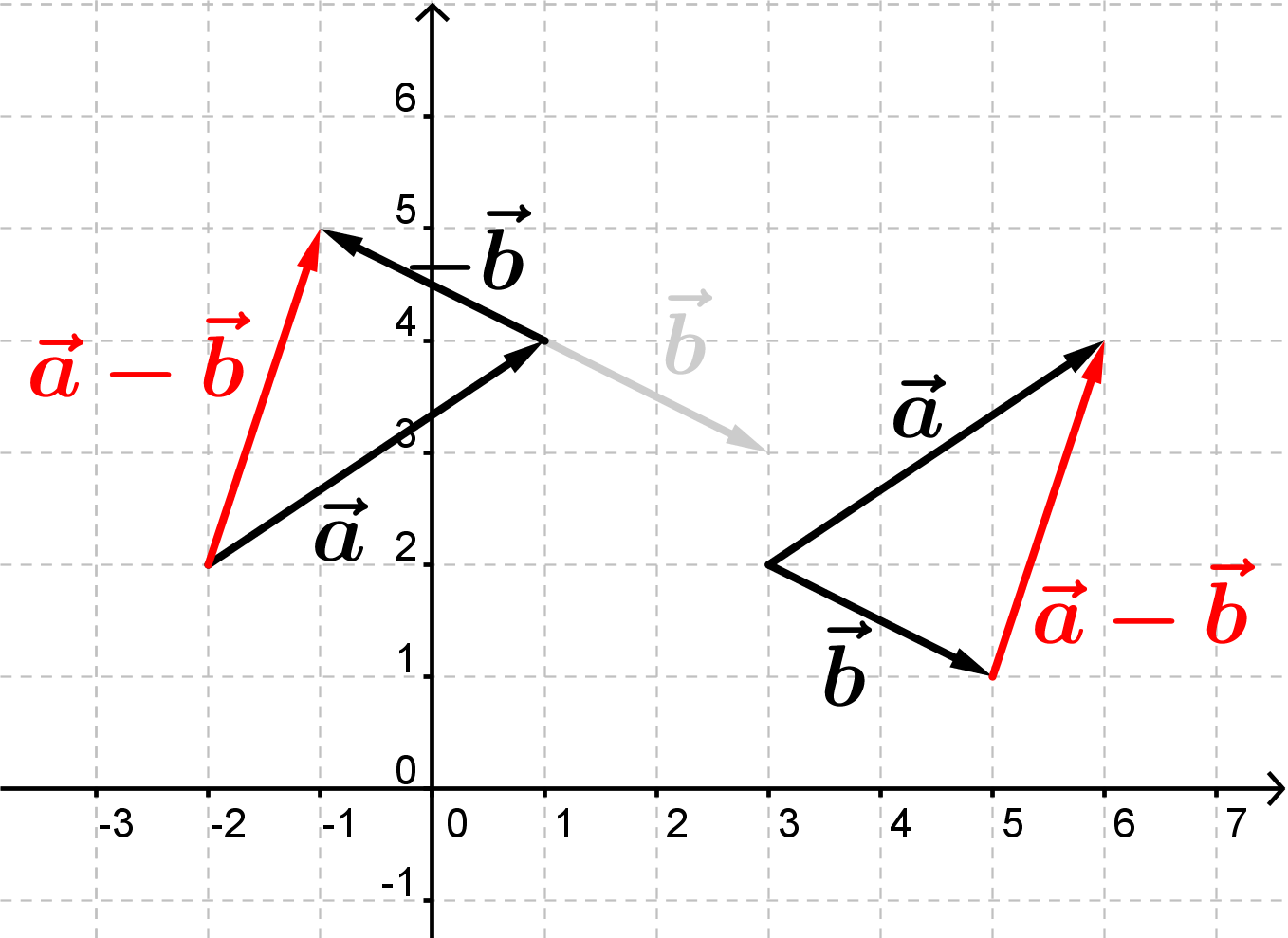
Der findes to måder at forklare det på grafisk.
Ved den første tegner man vektor a og i forlængelse af den tegner man vektor b bare i modsat retning. Når man forbinder start og slutpunkt, får man vektordifferensen.
Ved den anden tegner man vektor a og vektor b, hvor man starter i samme punkt. Den vektor der starter i spidsen af b og slutter i spidsen af a er vektordifferensen.
Når man ganger et tal med en vektor, ganger man tallet ind på hver koordinat.
$$t\cdot\overrightarrow{a}=\begin{pmatrix}t\cdot a_1\\t\cdot a_2\end{pmatrix}\\$$
F.eks. er
$$5\cdot\begin{pmatrix}2\\3\end{pmatrix}=\begin{pmatrix}5\cdot2\\5\cdot3\end{pmatrix}=\begin{pmatrix}10\\15\end{pmatrix}$$
Grafisk svarer det til at forlænge/forkorte vektoren. Derfor kalder man ofte tallet, man ganger med for skaleringsfaktoren.

