Distanceformlen

Mens afstandsformlen bruges til at bestemme afstanden mellem to punkter, så bruges distanceformlen til at bestemme den korteste afstand mellem en ret linje og et punkt.

Vi kalder vores rette linje for l, og vores punkt for P. Da l er ret, har den ligningen y=ax+b, og P har koordinatsættet (x₁, y₁). Den korteste afstand mellem P og l er

$$\text{dist}(P,l)=\frac{|ax_1+b-y_1|}{\sqrt{a^2+1}}$$

Den korteste afstand betyder den vinkelrette afstand, som man kan se på tegningen nedenfor.

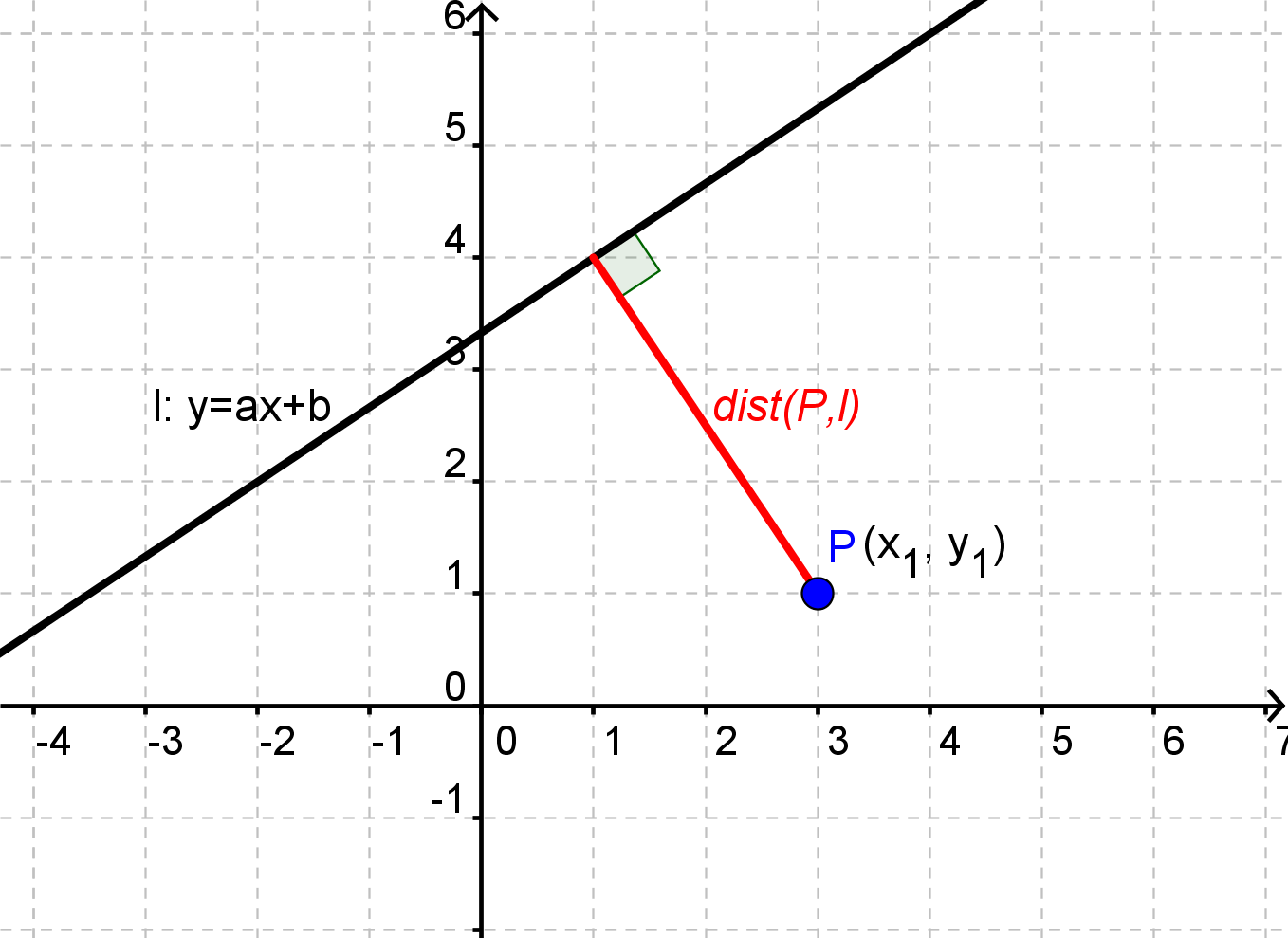
Hvis vores linje og punkt er givet ved

$$l:y=3x+2\quad \text{og}\quad P(5,\:7)$$

så er

$$\text{dist}(P,l)=\frac{|ax_1+b-y_1|}{\sqrt{a^2+1}}=\frac{|3\cdot5+2-7|}{\sqrt{3^2+1}}=\frac{|10|} {\sqrt{10}}=\frac{10}{\sqrt{10}}\approx3,16$$

Videolektion