Cirklens ligning
$$y=5x-3$$
er ligningen for en ret linje. Det betyder, at hvis man sætter et punkt (x, y) ind i ligningen, så vil ligningen være sand (der står det samme på begge sider af lighedstegnet) hvis punktet ligger på linjen, og den vil være falsk (der står noget forskelligt på de to sider) hvis punktet ikke ligger på linjen.
På samme måde kan man lave en ligning for en cirkel. En cirkel er bestemt ud fra to ting: dens centrum og dens radius.

Hvis et punkt P(x,y) ligger på cirklens periferi, så er afstanden mellem punktet og centrum lig med radius.
$$|PC|=r$$
Vi kan bruge afstandsformlen til at skrive lidt om på det.
$$|PC|=r$$
$$\sqrt{(x-a)^2+(y-b)^2}=r$$
$$(x-a)^2+(y-b)^2=r^2$$
Den nederste ligning er den, vi kalder for cirklens ligning. Hvis en cirkel har centrum i C(a, b) og radius r, så er dens ligning
$$(x-a)^2+(y-b)^2=r^2$$
Det vil sige, at et punkt P(x, y) ligger på cirklen hvis og kun hvis koordinatsættet (x, y) tilfredsstiller ligningen.
Eksempel
Cirklen med centrum i (1, 4) og med r=5 har ligningen
$$(x-1)^2+(y-4)^2=25$$
Punktet A(4, 8) ligger på cirkelens periferi, fordi
$$(4-1)^2+(8-4)^2=3^2+4^2=9+16=25=r^2$$
Punktet B(2,-1) ligger ikke på cirkelens periferi, fordi
$$(2-1)^2+(-1-4)^2=1^2+(-5)^2=1+25=26\neq r^2$$
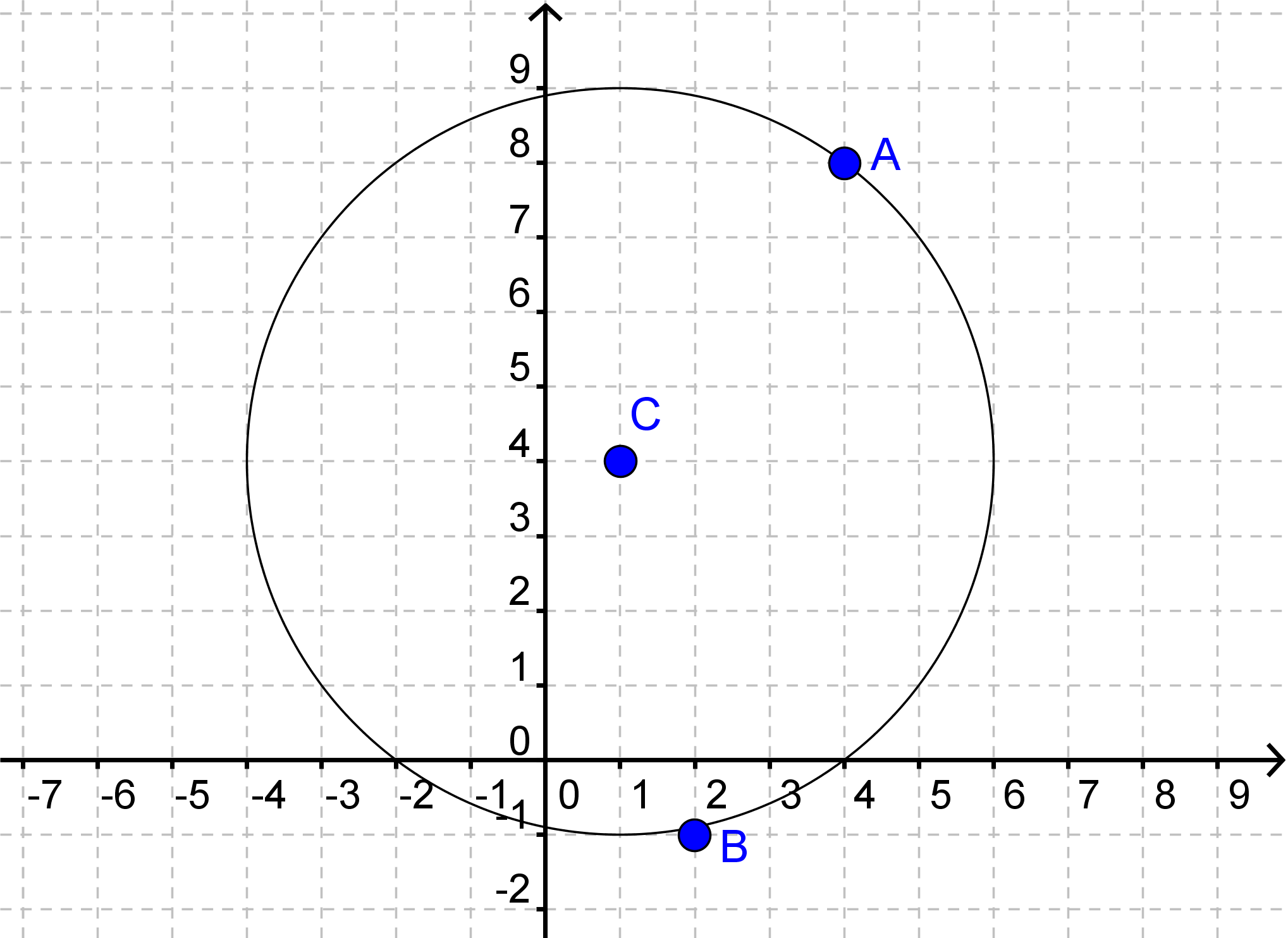
Cirklen og punkterne er indtegnet på figuren nedenfor