Andengradsuligheder

Du har måske tidligere kigget på andengradsligninger. Disse ligninger kan typisk skrives på formen:

\(0=ax^2+bx+c\)

For at løse denne har du måske brugt formlen: \(d=b^2-4\cdot a\cdot c\) til at finde diskriminanten, og derefter løst andengradsligningen ved: \(x=\frac{-b\pm\sqrt{d}}{2a}\)

Andengradsuligheder adskiller sig dog lidt. Disse kan skrives på formen:

\(0\neq ax^2+bx+c\)

Dette betyder at udtrykket \(ax^2+bx+c\) ikke er lig 0, men kan for eksempel være større end eller mindre end 0. Ved andengradsuligheder kan man møde de fire tilfælde:

\(0<ax^2+bx+c\)

\(0\leq ax^2+bx+c\)

\(0>ax^2+bx+c\)

\(0\geq ax^2+bx+c\)

Alle disse tilfælde løses ved først at løse den almindelige andengradsligning \(0=ax^2+bx+c\), og derefter finde intervallerne, hvor uligheden passer.

Eksempel

Vi er givet andengradsuligheden  \(0\leq 2x^2+2x-4\). For at løse den løser vi først andengradsligningen \(0=2x^2+2x-4\). Vi starter med, at finde diskriminanten

\(d=2^2-4\cdot 2\cdot (-4)\)

\(d=36\)

Nu kan vi så finde nulpunkterne:

\(x=\frac{-2\pm\sqrt{36}}{2\cdot 2}\)

\(x=1 \vee x=-2\)

Det kunne nu være interessant at tegne grafen:

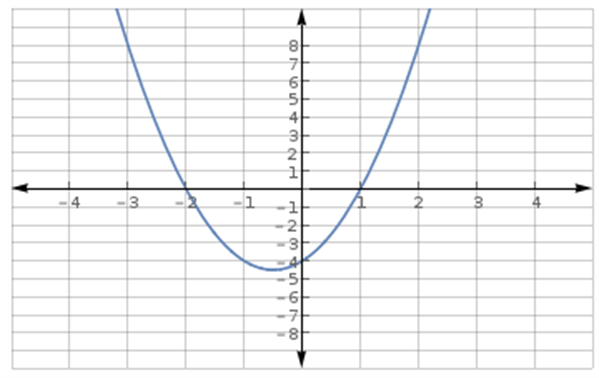
Vi vender nu tilbage til vores ulighed \(0\leq 2x^2+2x-4\). Vi leder efter x-værdier, der gør, at værdien af højresiden bliver større end eller lig 0. Ud fra grafen kan vi se, at værdien bliver under 0, hvis \(-2<x<1\). Løsningen for denne andengradsulighed er derfor:

$$L : ]\infty;-2] \wedge [1;\infty]$$