Dobbelte uligheder

Når man arbejder med uligheder, vurderer man altid i hvilket interval, det giver mening at betragte uligheden. Intervaller kan opskrives på to måder:

$$x \in \mathbb{R}| \, b<x<a \qquad \mathrm{eller} \qquad ]b;a]$$

Intervaller opdeles i åbne, halvåbne og lukkede intervaller (se mængdebyggeren og symboler). 

Grafisk markeres åbne intervaller med symbolet  \("\circ"\) og lukkede intervaller markeres med symbolet \("\bullet"\).

Grafisk ser det sådan ud:

Når man skal løse uligheder, kan man møde både lukkede, halvåbne og åbne intervaller:

$$\begin{align} a<x<b &= ]a,b[ \\ a \leq x < b &=[a,b[ \\a< x\leq b &= ]a,b] \\ a \leq x \leq b &= [a,b]\end{align}$$

En dobbeltulighed indeholder to ulighedstegn, som vender samme vej. Nu ser vi på, hvordan vi løser sådan en ulighed:

Vi skal løse denne dobbeltudlighed \(4x - 14 < 18x + 20 < 35x - 15\). For at gøre det, deler vi den op i to uligheder: \(4x - 14 < 18x + 20 \) og \(18x + 20 < 35x - 15\).

Vi betragter først \(4x - 14 < 18x + 20 \). Vi rykker rundt på leddene og reducerer: 

Ud fra det kan vi konkludere, at x skal være større end -2,4.

Så ser vi på den næste ulighed, nemlig \(18x + 20 < 35x - 15\), som vi behandler på samme måde: 

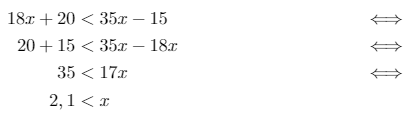
Ud fra det kan vi konkludere, at x skal være større end 2,1.

Når x er større end 2,1, er x automatisk også større end -2,4, så løsningen på uligheden er \(L= \{ x \in \mathbb{R} | x > 2,1 \} = ]2,1;\infty[ \)

Grafisk ser løsningen sådan ud: Her viser den blå markering  løsningen til første del af uligheden, mens den røde viser løsningen til anden del. Den grønne viser den samlede løsning.