At halvere en vinkel

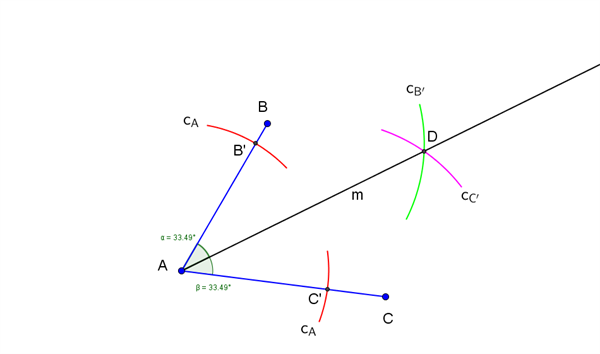
Der er givet en vinkel (\(\angle BAC\)) med toppunkt i punkt \(A\) og vinkelbenene \(AB\) og \(AC\) som vist med blåt i figuren. Vi skal halvere vinklen, dvs. konstruere en linje (\(m\)) i vinkelrummet mellem de to vinkelben, der deler vinkel \(\angle BAC\)) i to lige store vinkler.

Figur           At halvere en vinkel

Fremgangsmåde, se figuren:

1. tegn – med centrum i punkt \(A\) – en cirkel (\(c_A\)) med en selvvalgt radius (i figuren er kun vist de to cirkelbuer (røde) hørende til cirklen \(c_A\), som skærer de to vinkelben)
2. skæringspunkterne mellem cirklen \(c_A\) og vinkelbenene \(AB\) og \(AC\) betegnes hhv. \(B\:’\) og \(C\:’\)
3. tegn – med centrum i punkt \(B\:’\) – en cirkel (\(c_{B\:’}\)) med en selvvalgt radius, og bevar radius på din passer (i figuren er kun vist den cirkelbue (grøn) hørende til cirklen \(c_{B\:’}\), som er midt i vinkelrummet mellem de to vinkelben)
4. tegn – med centrum i punkt \(C\:’\) – en cirkel (\(c_{C\:’}\)) med samme radius som i cirklen \(c_{B\:’}\) (i figuren er kun vist den cirkelbue (lyserød) hørende til cirklen \(c_{C\:’}\), som er midt i vinkelrummet mellem de to vinkelben og skærer cirkelbuen hørende til cirklen \(c_{B\:’}\))
5. skæringspunktet mellem cirkelbuerne hørende til cirklerne \(c_{B\:’}\) og \(c_{C\:’}\)  betegnes \(D\)
6. halvlinjen (\(m\)) fra punkt \(A\) gennem punkt \(D\) er den ønskede vinkelhalveringslinje i vinkelrummet mellem de to vinkelben, der deler vinkel \(\angle BAC\) i to lige store vinkler.