Konstruktion af trekanter
Metoden for konstruktion af en trekant afhænger af, hvilke sidelængder og vinkler, der er kendt. I denne introduktionsvideo gennemgås de forskellige scenarier:
Til hvert scenarie hører en separat videolektion.
Alle tre sidelængder i trekanten er kendt
Der er givet en trekant \(ABC\), hvor vi kender alle tre sidelængder: \(a\), \(b\) og \(c\). For at fastlægge trekanten tager vi udgangspunkt i et koordinatsystem, hvor punkt \(A\) ligger i Origo, og punkt \(C\) ligger på x-aksen med x-koordinaten \(b\), som vist med blåt i figur 1.
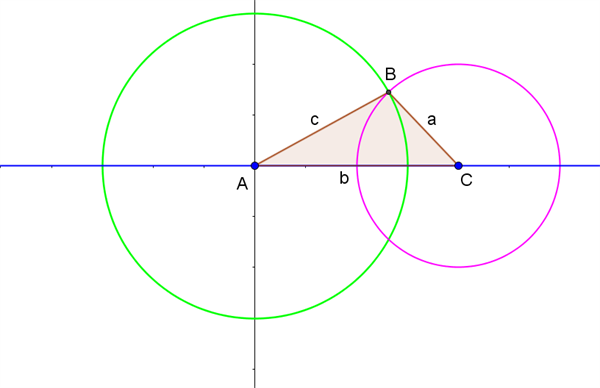
Figur 1 Konstruktion af trekant med alle tre sidelængder kendt
Geometrisk løsning
Vi kender sidelængden \(c\), og dermed ved vi, at punkt \(B\) må ligge på periferien af en cirkel med centrum i punkt \(A\) og radius \(c\). Cirklen er tegnet med grønt i figur 1.
Vi kender også sidelængden \(a\), og dermed ved vi, at punkt \(B\) må ligge på periferien af en cirkel med centrum i punkt \(C\) og radius \(a\). Cirklen er tegnet med lyserød i figur 1.
Vi kan dermed konstruere trekanten geometrisk, idet punkt \(B\) er skæringspunkt mellem de to cirkler. Der er egentlig to løsninger, idet punkt \(B\) også kan spejles i x-aksen og ligge under linjestykket \(AC\), men det ses i figur 1, at dette vil give en trekant, der er kongruent med trekant \(ABC\), så vi nøjes med at beskrive trekant \(ABC\) som løsningen.
Hvis summen af sidelængderne \(a\) og \(c\) er mindre end sidelængden \(b\), vil de to cirkler ikke skære hinanden. Konklusionen bliver i dette tilfælde, at trekanten ikke kan konstrueres, og de opgivne sidelængder repræsenterer dermed ikke en trekant.
Analytisk løsning
Vi kan også fastlægge placeringen af punkt \(B\) analytisk. Den grønne cirkel i figur 1 har ligningen:
\((x-0)^2+(y-0)^2=x^2+y^2=c^2\)
Og den lyserøde cirkel i figur 1 har ligningen:
\((x-b)^2+(y-0)^2=x^2+b^2-2\cdot b\cdot x+y^2=a^2\)
Ud fra disse to ligninger kan vi bestemme koordinaterne til punkt \(B\:(x_B, y_B)\), som opfylder begge ligninger. Hvis vi trækker de to venstresider fra hinanden, får vi:
\(x^2+y^2-(x^2+b^2-2\cdot b\cdot x+y^2)=c^2-a^2\)
\(2\cdot b\cdot x_B-b^2=c^2-a^2\)
Her kan vi isolere \(x_B\) og derefter benytte den øverste ligning til bestemmelse af \(y_B\):
\(x_B=\dfrac{b^2+c^2-a^2}{2\cdot b}\) og \(y_B=\sqrt{c^2-x_b^2}\)
Videolektion
I denne videolektion gennemgås begge løsningsmetoder.
Længden af to sider i trekanten og den mellemliggende vinkel er kendt
Der er givet en trekant \(ABC\), hvor vi kender to sidelængder og den mellemliggende vinkel. I eksemplet her forudsætter vi, at vi kender sidelængderne \(b\) og \(c\) og den mellemliggende vinkel \(A\). Tilsvarende fremgangsmåde kan benyttes, hvis det er andre sidelængder og deres mellemliggende vinkel, der er kendt.
For at fastlægge trekanten tager vi udgangspunkt i et koordinatsystem, hvor punkt \(A\) ligger i Origo, og punkt \(C\) ligger på x-aksen med x-koordinaten \(b\), som vist med blåt i figur 2.
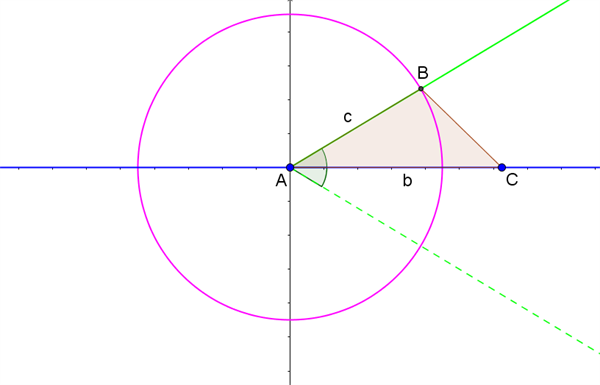
Figur 2 Konstruktion af trekant med længden af to sider og den mellemliggende vinkel kendt
Geometrisk løsning
Vi kender vinkel \(A\), og dermed ved vi, at punkt \(B\) må ligge på en halvlinje fra punkt \(A\), der danner denne vinkel med x-aksen. Halvlinjen er tegnet fuldt optrukkent med grønt i figur 2.
Vi kender også sidelængden \(c\), og dermed ved vi, at punkt \(B\) må ligge på periferien af en cirkel med centrum i punkt \(A\) og radius \(c\). Cirklen er tegnet med lyserød i figur 2.
Vi kan dermed konstruere trekanten geometrisk, idet punkt \(B\) er skæringspunkt mellem den fuldt optrukne halvlinje og cirklen. Der er egentlig to løsninger, idet punkt \(B\) også kan spejles i x-aksen og ligge under linjestykket \(AC\). Men det ses i figur 2, jf. den stiplede halvlinje, at dette vil give en trekant, der er kongruent med trekant \(ABC\), så vi nøjes med at beskrive trekant \(ABC\) som løsningen.
Uanset størrelsesforholdet mellem sidelængderne \(b\) og \(c\) og vinkel \(A\) vil der altid være en løsning til placeringen af punkt \(B\), og trekanten \(ABC\) vil altid kunne konstrueres.
Analytisk løsning
Vi kan også fastlægge placeringen af punkt \(B\) analytisk. Den grønne, fuldt optrukne halvlinje i figur 2 har parameterfremstillingen:
\((x,y)=(t\cdot \cos(A), t\cdot \sin(A)), t\ge 0\)
Den lyserøde cirkel i figur 2 har ligningen:
\((x-0)^2+(y-0)^2=x^2+y^2=c^2\)
Ud fra disse to ligninger kan vi bestemme koordinaterne til punkt \(B\: (x_B, y_B)\), som opfylder begge ligninger. Vi indsætter parameterfremstillingen for halvlinjen i cirklens ligning:
\(t^2\cdot \cos^2(A) + t^2\cdot \sin^2(A) = t^2\cdot (\cos^2(A) + \sin^2(A)) = c^2\)
Her udnytter vi, at \(\cos^2(A) + \sin^2(A) =1\) og får, at \(t^2=c^2\) eller \(t=c\), således at:
\((x_B,y_B)=(c\cdot \cos(A), c\cdot \sin(A))\)
Videolektion
I denne videolektion gennemgås begge løsningsmetoder:
To vinkler i trekanten og længden af den mellemliggende side er kendt
Der er givet en trekant \(ABC\), hvor vi kender to vinkler og den mellemliggende side. I eksemplet her forudsætter vi, at vi kender vinklerne \(A\) og \(C\) og sidelængden \(b\). Tilsvarende fremgangsmåde kan benyttes, hvis det er andre vinkler og/eller sidelængder, der er kendt.
For at fastlægge trekanten tager vi udgangspunkt i et koordinatsystem, hvor punkt \(A\) ligger i Origo, og punkt \(C\) ligger på x-aksen med x-koordinaten \(b\), som vist med blåt i figur 3.
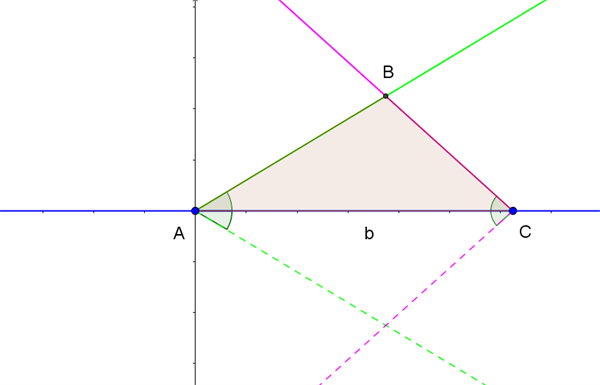
Figur 3 Konstruktion af trekant med to vinkler og den mellemliggende side kendt
Geometrisk løsning
Vi kender vinkel \(A\), og dermed ved vi, at punkt \(B\) må ligge på en halvlinje fra punkt \(A\), der danner denne vinkel med x-aksen. Halvlinjen er tegnet fuldt optrukkent med grønt i figur 3.
Vi kender også vinkel \(C\), og dermed ved vi, at punkt \(B\) må ligge på en halvlinje fra punkt \(C\), der danner denne vinkel med x-aksen. Halvlinjen er tegnet fuldt optrukkent med lyserød i figur 3.
Vi kan dermed konstruere trekanten geometrisk, idet punkt \(B\) er skæringspunkt mellem de to fuldt optrukne halvlinjer. Der er egentlig to løsninger, idet punkt \(B\) også kan spejles i x-aksen og ligge under linjestykket \(AC\). Men det ses i figur 3, jf. de stiplede halvlinjer, at dette vil give en trekant, der er kongruent med trekant \(ABC\), så vi nøjes med at beskrive trekant \(ABC\) som løsningen.
Hvis summen af vinkel \(A\) og vinkel \(C\) er 180° eller mere, vil de to halvlinjer ikke skære hinanden, og konklusionen bliver i så fald, at trekanten ikke kan konstrueres, og den opgivne sidelængde sammen med de opgivne vinkler repræsenterer dermed ikke en trekant. Det ville vi også kunne konkludere alene ud fra reglen om vinkelsummen i en trekant.
Analytisk løsning
Vi kan også fastlægge placeringen af punkt \(B\) analytisk. Den fuldt optrukne grønne halvlinje i figur 3 har parameterfremstillingen:
\((x,y)=(t_1\cdot \cos(A), t_1\cdot \sin(A)), t_1\ge 0\)
Den fuldt optrukne lyserøde halvlinje i figur 3 har parameterfremstillingen:
\((x,y)=(b-t_2\cdot \cos(C), t_2\cdot \sin(C)), t_2\ge 0\)
Ud fra disse to ligninger kan vi bestemme koordinaterne til punkt \(B\: (x_B, y_B)\), som opfylder begge ligninger. Vi starter med y-koordinaten:
\(t_1\cdot \sin(A) = t_2\cdot \sin(C))\) og dermed: \(t_2 = t_1\cdot \dfrac{\sin(A)}{\sin(C)}\)
Vi indsætter dette i x-koordinaten:
\(t_1\cdot \cos(A) = b - t_1\cdot \dfrac{\sin(A)}{\sin(C)}\cdot \cos(C)\) og dermed:
\(t_1 =\dfrac{b}{\cos(A) + \frac{\sin(A)\: \cdot \:\cos(C)}{\sin(C)}} = \dfrac{b\cdot \sin(C)}{\cos(A)\cdot \sin(C) + \sin(A)\cdot \cos(C)}\)
Her har vi sat nævneren på fællesnævner og ganget nævneren’s nævner op i tælleren (vi dividerer med en brøk ved at gange med den omvendte).
Vi bestemmer herefter \(t_2\) og koordinaterne til punkt \(B\):
\(t_2 = \dfrac{b\cdot \sin(A)}{\cos(A)\cdot \sin(C) + \sin(A)\cdot \cos(C)}\)
\((x_B,y_B)=(t_1\cdot \cos(A), t_1\cdot \sin(A))\)
\(= (\dfrac{b\cdot \sin(C)\cdot \cos(A)}{\cos(A)\cdot \sin(C) + \sin(A)\cdot \cos(C)}, \dfrac{b\cdot \sin(C)\cdot \sin(A)}{\cos(A)\cdot \sin(C) + \sin(A)\cdot \cos(C)})\)
Videolektion:
I denne videolektion gennemgås begge løsningsmetoder.
Længden af en side, den modstående vinkel samt yderligere en vinkel i trekanten er kendt
Der er givet en trekant \(ABC\), hvor vi kender en sidelængde, den modstående vinkel og yderligere en vinkel. Vi benytter reglen om vinkelsummen i en trekant til at beregne den tredje vinkel som 180° minus summen af de to kendte vinkler. Herefter kan vi benytte fremgangsmåden i forrige afsnit til at fastlægge/konstruere trekanten, idet vi nu kender vinklen i begge ender af den kendte sidelængde.
Længden af en side, den modstående vinkel samt yderligere en sidelængde i trekanten er kendt
Der er givet en trekant \(ABC\), hvor vi kender en sidelængde, den modstående vinkel og yderligere en sidelængde. I eksemplet her forudsætter vi, at vi kender vinkel \(A\) og sidelængderne \(a\) og \(b\). Tilsvarende fremgangsmåde kan benyttes, hvis det er en anden vinkel og/eller andre sidelængder, der er kendte.
For at fastlægge trekanten tager vi udgangspunkt i et koordinatsystem, hvor punkt \(A\) ligger i Origo, og punkt \(C\) ligger på x-aksen med x-koordinaten \(b\), som vist med blåt i figur 4.
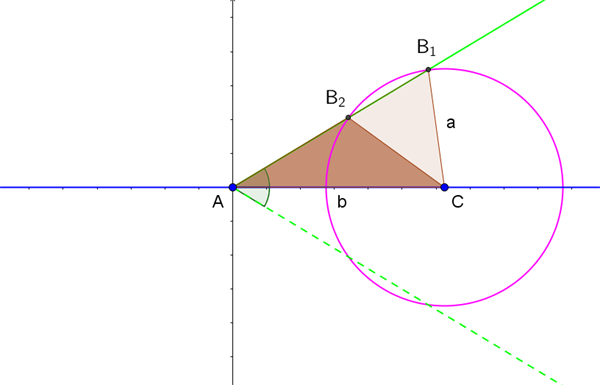
Figur 4 Konstruktion af trekant med længden af en side, den modstående vinkel samt yderligere en sidelængde kendt
Geometrisk løsning
Vi kender vinkel \(A\), og dermed ved vi, at punkt \(B\) må ligge på en halvlinje fra punkt \(A\), der danner denne vinkel med x-aksen. Halvlinjen er tegnet fuldt optrukkent med grønt i figur 4. (Vi forudsætter i første omgang, at vinkel \(A\) er spids og at \(a < b\)).
Vi kender også sidelængden \(a\), og dermed ved vi, at punkt \(B\) må ligge på periferien af en cirkel med centrum i punkt \(C\) og radius \(a\). Denne cirkel er tegnet med lyserød i figur 4.
Vi kan dermed konstruere trekanten geometrisk, idet punkt \(B\) er skæringspunkt mellem den fuldt optrukne halvlinje og cirklen. Skæringspunkterne giver her to forskellige løsninger til trekanten, henholdsvis trekant \(AB_1C\), hvori vinkel \(B\) er spids, og trekant \(AB_2C\), hvori vinkel \(B\) er stump. Der er egentlig fire løsninger, idet punkt \(B\) også kan spejles i x-aksen og ligge under linjestykket \(AC\). Men det ses i figur 4, jf. den stiplede halvlinje, at dette vil give to trekanter, der er kongruente med trekanterne \(AB_1C\) og \(AB_2C\), så vi nøjes med at beskrive disse to trekanter som løsningen.
I et særligt tilfælde er punkt \(B_1\) og punkt \(B_2\) sammenfaldende, og de to løsninger smelter sammen til én og samme trekant. Her er halvlinjen tangent til cirklen, hvilket opnås, når \(\sin(A) = \dfrac{a}{b}\). Løsningen er en retvinklet trekant, hvori vinkel \(B\) er den rette vinkel.
Hvis \(\sin(A) > \dfrac{a}{b}\), vil halvlinjen og cirklen ikke skære hinanden. Konklusionen bliver i dette tilfælde, at trekanten ikke kan konstrueres, og de opgivne sidelængder sammen med den opgivne vinkel repræsenterer dermed ikke en trekant.
Hvis vinkel \(A\) er spids og \(a \ge b\), er der kun ét skæringspunkt mellem halvlinjen og cirklen (svarende til punkt \(B_1\)) og dermed kun én trekant \(AB_1C\) som løsning, hvori vinkel B er spids.
Hvis vinkel \(A\) er ret eller stump, vil halvlinjen i punkt \(A\) med retning mod punkt \(B\) enten være lodret eller være rettet mod venstre i figur 4. Hvis \(a > b\), ses der i dette tilfælde kun at være ét skæringspunkt mellem halvlinjen og cirklen (svarende til punkt \(B_1\)) og dermed kun én trekant \(AB_1C\) som løsning.
Hvis vinkel \(A\) er ret eller stump og \(a \le b\), vil halvlinjen og cirklen ikke skære hinanden, og konklusionen bliver i så fald, at trekanten ikke kan konstrueres, og de opgivne sidelængder sammen med den opgivne vinkel repræsenterer dermed ikke en trekant.
Analytisk løsning
Vi kan også fastlægge placeringen af punkt \(B\) analytisk. Den fuldt optrukne grønne halvlinje i figur 4 har parameterfremstillingen:
\((x,y)=(t_1\cdot \cos(A), t_1\cdot \sin(A)), t_1\ge 0\)
Den lyserøde cirkel i figur 4 har ligningen:
\((x-b)^2+(y-0)^2=x^2+b^2-2\cdot b\cdot x+y^2=a^2\)
Ud fra disse to ligninger kan vi bestemme koordinaterne til punkt \(B\: (x_B, y_B)\), som opfylder begge ligninger. Vi indsætter parameterfremstillingen for halvlinjen i cirklens ligning:
\(t_1^2\cdot\cos^2(A)+b^2-2\cdot b\cdot t_1\cdot\cos(A)+t_1^2\cdot\sin^2(A)=a^2\)
Dette giver en andengradsligning i \(t_1\), og vi udnytter, at \(\cos^2(A) + \sin^2(A) =1\):
\(t_1^2 -2\cdot b\cdot\cos(A)\cdot t_1+(b^2-a^2)=0\)
Vi beregner diskriminanten, udnytter igen \(\cos^2(A) + \sin^2(A) =1\) og en kvadratsætning:
\(d=(-2\cdot b\cdot\cos(A))^2-4\cdot 1\cdot (b^2-a^2)=4\cdot b^2\cdot (\cos^2(A)-1+\dfrac{a^2}{b^2})\)
\(=4\cdot b^2\cdot(\dfrac{a^2}{b^2}-\sin^2(A))=4\cdot b^2\cdot (\dfrac{a}{b}+\sin(A))\cdot (\dfrac{a}{b}-\sin(A))\)
Andengradsligningens løsning(er) er:
\(t_1=\dfrac{2\cdot b\cdot\cos(A)\pm\sqrt{4\cdot b^2\cdot (\dfrac{a}{b}+\sin(A))\cdot (\dfrac{a}{b}-\sin(A))}}{2\cdot 1}\)
\(=b\cdot\Big\{\cos(A)\pm\sqrt{(\dfrac{a}{b}+\sin(A))\cdot (\dfrac{a}{b}-\sin(A))}\Big\}\)
Og:
\((x_B,y_B)=(t_1\cdot \cos(A), t_1\cdot \sin(A))\)
Fortegnet for udtrykket under kvadratrodstegnet til bestemmelse af \(t_1\) sammen med betingelsen, at kun positive værdier af \(t_1\) kan bruges, afgør antallet af løsninger til placeringen af punkt \(B\):
- hvis \(a < b\) og \(\cos(A) > 0\) svarende til, at vinkel \(A\) er spids:
- hvis \(\sin(A) < \dfrac{a}{b}\) er der to løsninger til placeringen af punkt \(B\)
- hvis \(\sin(A) = \dfrac{a}{b}\) er der kun én løsning til placeringen af punkt \(B\)
- hvis \(\sin(A) > \dfrac{a}{b}\) er der ingen løsning til placeringen af punkt \(B\)
- hvis \(a = b\) og \(\cos(A) > 0\) svarende til, at vinkel \(A\) er spids, er der kun én løsning til placeringen af punkt \(B\)
- hvis \(a \le b\) og \(\cos(A) \le 0\) svarende til, at vinkel \(A\) er ret eller stump, er der ingen løsning til placeringen af punkt \(B\)
- hvis \(a > b\) er der kun én løsning til placeringen af punkt \(B\), uanset om vinkel \(A\) er spids, ret eller stump
Videolektion
I denne videolektion gennemgås begge løsningsmetoder.
