Trigonometriske uligheder

Trigonometriske uligheder er udtryk på formen

$$\cos(v) \geq k \\
\sin(v) \geq k \\
\tan(v) \geq k$$

 Lad os igen beskrive metoden for én type af gangen.

Cosinus

Hvis vi skal løse uligheden \( \cos(v) \geq 0,3 \), husker vi igen på, at cosinus til en vinkel er \( x \)-værdien for et punkt på enhedscirklen. Det vil sige, at alle de vinkler der opfylder, at \( \cos(v) \geq 0,3 \), kan findes som vinklerne markeret med rød i figuren nedenfor.

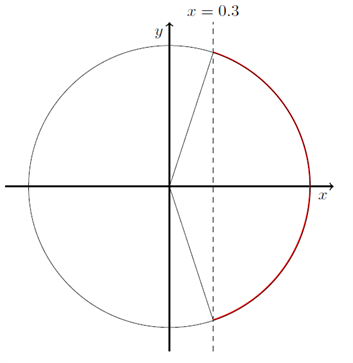
I afsnittet om trigonometriske grundligninger bestemte vi løsningerne til ligningen \( \cos(v) = 0,3 \), og vi fandt, at løsningerne var \( 1,26 \) og \( 5,01 \) radianer.

Løsninger til \( \cos(v) \geq 0,3 \) er præcis punkter på enhedscirklen, der har \( x \)-værdi større end \( 0,3 \). Det vil sige, at vi skal have de vinkler, der ligger imellem 1,26 radianer og 5,01 radianer. Dermed bliver løsningerne de vinkler, der er mindre end 1,26, og større end 5,01 radianer. Hvis vi skriver det i intervaller, bliver løsningerne

$$ [0;1.26] \cup [5.01,2\pi]$$

Her betyder \( \cup \), at løsningerne bliver de vinkler, der enten ligger i  \( [0;1.26] \)  eller \( [5.01,2\pi] \) opfylder den ønskede ulighed.

Sinus

Hvis vi skal løse uligheden \( \sin(v) \geq 0,3 \), husker vi igen på, at sinus til en vinkel er \( y \)-værdien for et punkt på enhedscirklen. Det vil sige, at alle de vinkler der opfylder, at \( \sin(v) \geq 0,3 \), kan findes som vinklerne markeret med rød i figuren nedenfor.

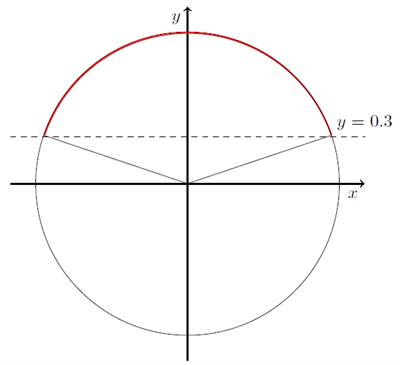
I afsnittet om trigonometriske grundligninger bestemte vi løsningerne til ligningen \( \sin(v) = 0,3 \), og vi fandt, at løsningerne var \( 0,33 \) og \( 2,81 \) radianer.

Løsninger til \( \sin(v) \geq 0,3 \) er præcis punkter på enhedscirklen, der har \( y \)-værdi større end \( 0,3 \). Det vil sige, vi skal have de vinkler, der ligger imellem 0,33 radianer og 2,81 radianer. Dermed bliver løsningerne de vinkler, der er større end 0,33 og mindre end 2,81. Hvis vi skriver det i intervaller, bliver løsningerne

$$ [0.33;2.81] $$

Tangens

Vi ønsker nu at løse uligheden \( \tan(v) \geq 1,7 \). Vi har allerede løst den trigonometriske lighed \( \tan(v) = 1.7 \), løsningerne var \( 1,08 \) radianer og \( 4,22 \) radianer. Bemærk, at der vil være to områder, hvor uligheden gælder: Et område, der indeholder hver af de to vinkler, se eventuelt figuren nedenfor.

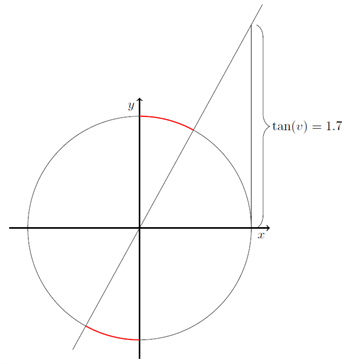
Vi vil starte med at tage udgangspunkt i den første vinkel, der løste ligheden \( \tan(v) = 1,7 \), det vil sige, vi betragter \( v = 1,08 \) radianer. Hvis vi gør vinklen en lille smule større, bliver tangens til vinklen også lidt større, da kateten modsat vinklen bliver længere. Det vil sige, vi skal blot finde ud af, hvornår tangens stopper med at vokse, når vinklen vokser. Dette sker netop, når vinklen bevæger sig over på den anden side af \( y \)-aksen, det vil sige, når vinklen bliver større end \( \frac{\pi}{2} \), bliver tangens negativ. Det vil sige, at alle vinklerne, der ligger mellem \( 1,08 \) radianer og \( \frac{\pi}{2} \) radianer opfylder, at \( \tan(v) \geq 1,7 \). 

Bemærk, at \( \frac{\pi}{2} \) ikke er med, da tangens slet ikke er defineret, når vinklen er lig \( \frac{\pi}{2} \) !

Det vil sige, at alle vinklerne i intervallet \( [1,08, \frac{\pi}{2} [ \) opfylder uligheden. For at finde de resterende vinkler, lægger vi blot \( \pi \) til alle vinklerne i intervallet, ( da \( \tan(v) = \tan( v + \pi) \) ). Det vil sige, at alle vinklerne, der opfylder, at \( \tan(v) \geq 1,7 \) er vinklerne i intervallet

$$ \left[1,08 ; \frac{\pi}{2} \right[ \cup \left[4.22 ; \frac{3 \pi}{2} \right[ $$