Krumning
For en graf anvender vi betegnelsen krumning til at beskrive, hvor meget grafen buer. I dette afsnit vil vi kvantificere grafens krumning og opstille et udtryk til at beregne krumningen.
I figur 1 er indtegnet et udsnit af en vilkårlig graf og en tilhørende tangent til grafen i punktet \(P(x, f(x)\).
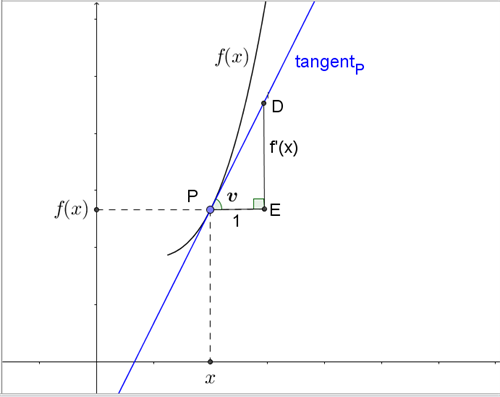
Figur 1 Grafen for en funktion med tangent i punkt \(P\)
Vi erindrer, at vi kan bestemme tangentens hældning ved at differentiere funktionen, og sammenhængen mellem tangentens hældning, \(f’(x)\), og den vinkel, \(v\), som tangenten danner med x-aksen, fremgår af den retvinklede trekant \(PDE\):
\(\tan(v) = \dfrac{f’(x)}{1} = f’(x)\)
For at bestemme hypotenusen i trekant \(PDE\) benyttes Pythagoras: \(PD = \sqrt{1+f’(x)^2}\) og dermed er \(\cos{v} = \frac{hosliggende \:katete}{hypotenusen} = \frac{1}{ \sqrt{1+f’(x)^2}}\).
Intuitivt betragtet, må grafens krumning have noget at gøre med, hvor meget tangentens hældning ændrer sig. Hvis hældningen ændrer sig meget, vil vi betegne krumningen som stor, og hvis hældningen kun ændrer sig lidt, vil vi betegne krumningen som lille. I grænsetilfældet, hvor grafens hældning er konstant, dvs. for en ret linje, vil det give mening at sige, at krumningen er 0.
Tangenthældningens ændring kan vi udtrykke matematisk som den anden afledede af funktionen:
\(\dfrac{d}{dx}(f’(x)) = \dfrac{d^2}{dx^2}(f(x)) = f’’(x)\)
I figur 2 har vi indtegnet en cirkel med centrum i et punkt \(C(x_C, y_C)\) (som vi endnu ikke kender) og radius \(R\) (som vi endnu heller ikke kender). Cirklen går gennem punkt \(P\), og i nærheden af \(x\) vil vi benytte denne cirkel – vi kan kalde den krumningscirklen – som en tilnærmelse til grafen for \(f(x)\).
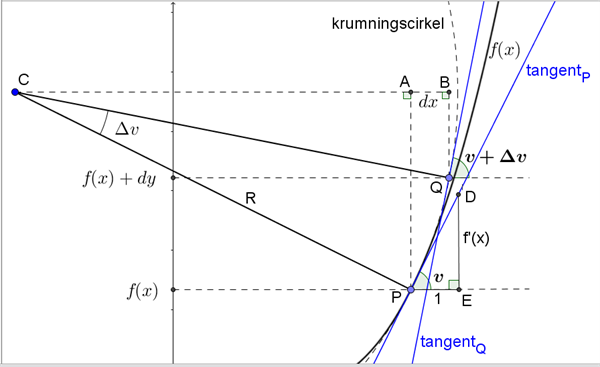
Figur 2 Grafen for en funktion med tilørende krumningscirkel
Ved en lille tilvækst \(dx\) til x-værdien bevæger vi os fra punktet \(P\) på cirklen til punktet \(Q(x+dx, f(x)+dy)\) på cirklen, hvor radius er drejet en vinkel, \(\Delta v\), i forhold til den radius, der går til punktet \(P\).
I ethvert punkt på en cirkel står tangenten vinkelret på radius, så i punkt \(Q\) er tangenten drejet \(\Delta v\) i forhold til tangenten i punkt \(P\). For tangenten i punkt \(Q\) gælder, idet \(dx\) er lille:
\(\tan{(v+\Delta v)} = f'(x+dx) = f’(x) + f’’(x)\cdot dx\)
Når \(\Delta v\) er lille, kan venstresiden tilsvarende omskrives, og idet \(\frac{d}{dv}(\tan{v}) = \frac{1}{\cos^2{v}}\), får vi:
\(\tan{(v+\Delta v)} = \tan{v} + \dfrac{d}{dv}(\tan{v})\cdot \Delta v = f’(x) + \dfrac{\Delta v}{\cos^2{v}}\)
Ved at sammenligne de to udtryk for \(\tan{(v+\Delta v)}\) og udnytte, at \(\cos{v} = \frac{1}{\sqrt{1+f’(x)^2}}\), fremkommer følgende sammenhæng mellem \(\Delta v\) og \(dx\):
\(\dfrac{\Delta v}{\cos^2{v}} = f’’(x)\cdot dx\implies \Delta v = f’’(x)\cdot \cos^2{v}\cdot dx = \dfrac{f’’(x)}{1+f’(x)^2}\cdot dx\)
Idet \(\angle CPA = v\) og \(\angle CQB = v+\Delta v\) i figur 2 gælder: \(CB = R\cdot \sin{(v+\Delta v)}\) og \(CA = R\cdot \sin{v}\) og dermed:
\(dx = CB - CA = R\cdot \Big(\sin{(v+\Delta v)} - \sin{v}\Big)\)
Når \(\Delta v\) er lille, og idet \(\frac{d}{dv}(\sin{v}) = \cos{v}\), får vi:
\(dx = R\cdot \Big(\sin{v} + \dfrac{d}{dv}(\sin{v})\cdot \Delta v - \sin{v}\Big) = R\cdot \Delta v\cdot \cos{v} \implies R = \dfrac{dx}{\Delta v\cdot \cos{v}}\)
Heri indsættes udtrykkene ovenfor for hhv. \(\Delta v\) og \(\cos{v}\). Herved kan \(dx\) forkortes ud, og vi får følgende udtryk for \(R\) som fuktion af x:
\(R(x) = \dfrac{(1 + f’(x)^2)\cdot \sqrt{1+f’(x)^2}}{f’’(x)} = \dfrac{(1 + f’(x)^2)^{1,5}}{f’’(x)} , f’’(x) \neq 0\)
\(R(x)\) er radius i krumningscirklen og kaldes for grafens krumningsradius i punktet \(x\). Vi indfører med det græske bogstav kappa, \(\kappa\), betegnelsen grafens krumning som den reciprokke krumningsradius:
\(\kappa(x) = \dfrac{1}{R(x)} = \dfrac{f’’(x)}{(1 + f’(x)^2)^{1,5}}\)
I overensstemmelse med vores intuitive betragtning i indledningen ser vi, at krumningen er proportional med \(f’’(x)\), dvs. proportional med ændringen af tangentens hældning. Når \(f’’(x)\) er stor, er krumningen stor, og når \(f’’(x)\) er lille, er krumningen lille.
En stor krumning modsvares af en lille krumningsradius og vice versa.
For den rette linje er \(f’’(x) = 0\), og dermed er krumningen \(\kappa(x) = 0\). Krumningsradius for den rette linje er ikke defineret, hvilket vi i nogle sammenhænge kan finde på at udtrykke som, at den rette linjes krumningsradius er uendelig stor.
Vi lægger mærke til, at både krumningsradius og krumning kan antage såvel positive som negative værdier alene afhængigt af fortegnet for \(f’’(x)\). Det giver ikke nogen mening, et en cirkel kan have en negativ radius, og det er da heller ikke tilfældet her. Fortegnet for krumningsradius og krumning fortæller, om krumningscirklens centrum ligger over eller under grafen. Krumningscirklens radius er således den numeriske værdi af \(R(x)\).
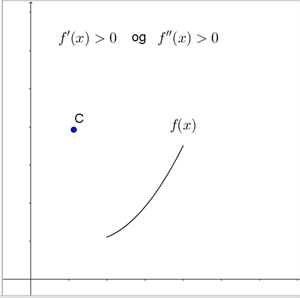
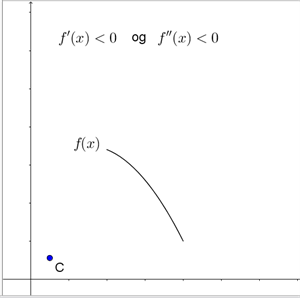
Når \(f’’(x)\) (og dermed krumningsradius og krumning) er positiv, er tangentens hældning voksende – i dette tilfælde bliver grafen enten stejlere for stigende x-værdier (hvis \(f’(x) > 0\)) eller fladere for stigende x-værdier (hvis \(f’(x) < 0\)). Her krummer grafen opad, og krumningscirklens centrum ligger over grafen, se figur 3 øverst.
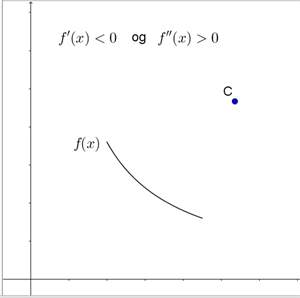
Når \(f’’(x)\) (og dermed krumningsradius og krumning) er negativ, er tangentens hældning aftagende – i dette tilfælde bliver grafen enten stejlere for stigende x-værdier (hvis \(f’(x) < 0\)) eller fladere for stigende x-værdier (hvis \(f’(x) > 0\)). Her krummer grafen nedad, og krumningscirklens centrum ligger under grafen, se figur 3 nederst.
 |
 |
 |
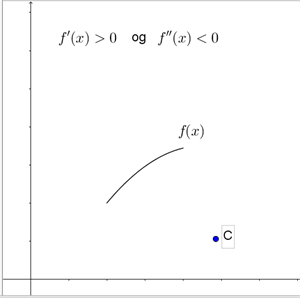 |
Figur 3 Placering af krumningscirklens centrum, afhængigt af fortegnet for \(f’(x)\) og \(f’’(x)\)
Afslutningsvis beregner vi beliggenheden af krumningscirklens centrum \(C\). Trekant \(PAC\) i figur 2 giver, idet \(\sin{v} = \frac{f’(x)}{\sqrt{1+f’(x)^2}}\) og \(\cos{v} = \frac{1}{\sqrt{1+f’(x)^2}}\):
\(x_C = x\: – R(x)\cdot \sin{v} = x\: – R(x)\cdot \dfrac{f’(x)}{\sqrt{1+f’(x)^2}} = x\: - \dfrac{1 + f’(x)^2}{f’’(x)}\cdot f’(x)\)
\(y_C = f(x) + R(x)\cdot \cos{v} = f(x) + R(x)\cdot \dfrac{1}{\sqrt{1+f’(x)^2}} = f(x) + \dfrac{1 + f’(x)^2}{f’’(x)}\)
\(f''(x) \neq 0\).
Eksempel 1: Cirklen
Cirklen er et godt eksempel at prøve teorien af på, for her kender vi faktisk resultatet på forhånd. Krumningscirklen må overalt være sammenfaldende med cirklen, så krumningsradius må være den samme som cirklens radius, og krumningscentrum må være sammenfaldende med cirklens centrum.
Ligningen for en cirkel med radius \(r\) og centrum i Origo (0,0) er som bekendt
\(x^2 + y^2 = r^2\implies y = \pm\sqrt{r^2 - x^2 }\)
Højresiden viser, at der for hver x-værdi er to tilhørende y-værdier, hvilket modsvarer hhv. den øvre halvcirkel og den nedre halvcirkel. Her vil vi indskrænke os til at kigge på den øvre halvcirkel med positiv y-værdi, \(f(x)\) i figur 4. Du kan selv foretage eftervisningen for den nedre halvcirkel med negative y-værdier, \(g(x)\) i figur 4.
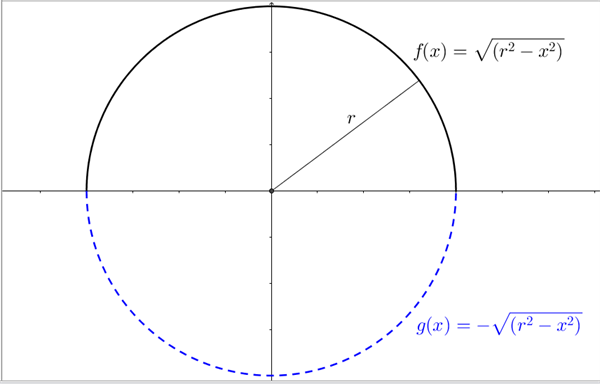
Figur 4 Cirkel med radius \(r\) og centrum i Origo (0,0) opdelt i to halvcirkler
\(f(x) = \sqrt{r^2 – x^2 }\)
\(f’(x) = \dfrac{– 2x}{2\cdot \sqrt{r^2 – x^2}} = \dfrac{– x}{\sqrt{r^2 – x^2}}\)
\(f’’(x) = \dfrac{– 1}{\sqrt{r^2 – x^2}} + \dfrac{(– x)\cdot (– 2x)}{(–2)\cdot (\sqrt{r^2 – x^2})^3} = \dfrac{– (r^2 – x^2) – x^2}{(r^2 – x^2)\cdot \sqrt{r^2 – x^2}} = \dfrac{– r^2}{(r^2 – x^2)^{1,5}}\)
Vi kan herefter bestemme krumningsradius og krumning:
\(R(x) = \dfrac{(1 + f’(x)^2)^{1,5}}{f’’(x)} = \dfrac{(1 + \frac{x^2}{r^2 – x^2})^{1,5}}{\frac{– r^2}{(r^2 – x^2)^{1,5}}} = \dfrac{(r^2)^{1,5}}{(r^2 – x^2)^{1,5}}\cdot \dfrac{(r^2 – x^2)^{1,5}}{– r^2} = \:– r\)
\(\kappa(x) = \dfrac{1}{R(x)} = \dfrac{– 1}{r}\)
Vi når altså frem til det forventede resultat.
At krumning og krumningsradius er negativ betyder, at krumningscentrum ligger under grafen, hvilket også passer med vores forventning om, at krumningscentrum skal ligge i Origo (0,0).
Dette kan vi også eftervise:
\(x_C = x \:– \dfrac{1 + f’(x)^2}{f’’(x)}\cdot f’(x) = x \:– \dfrac{1 + \frac{x^2}{r^2 – x^2}}{\frac{– r^2}{(r^2 – x^2)^{1,5}}}\cdot \dfrac{– x}{\sqrt{r^2 – x^2}}\)
\(= x \:– \dfrac{r^2}{r^2 – x^2}\cdot \dfrac{(r^2 – x^2)^{1,5}}{– r^2}\cdot \dfrac{– x}{\sqrt{r^2 – x^2}} = x \:– x = 0\)
\(y_C = f(x) + \dfrac{1 + f’(x)^2}{f’’(x)} = f(x) + \dfrac{1 + \frac{x^2}{r^2 – x^2}}{\frac{– r^2}{(r^2 – x^2)^{1,5}}}\)
\(= f(x) + \dfrac{r^2}{r^2 – x^2}\cdot \dfrac{(r^2 – x^2)^{1,5}}{– r^2} = f(x) \:– \sqrt{r^2 – x^2} = f(x) \:– f(x) = 0\)
Eksempel 2 Sinuskurve
Lad os kigge på sinuskurven med amplituden 1, se figur 5.
\(f(x) = \sin(x), 0\leq x \leq 2\pi\)
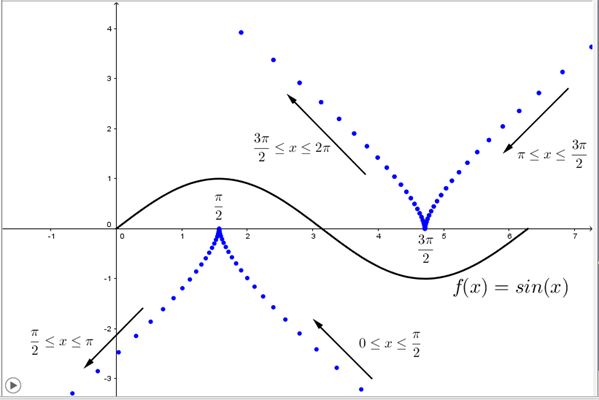
Figur 5 Sinuskurve med amplituden 1, og krumningscirklers centrum indtegnet med blåt
Vi vil bestemme krumningsradius, krumning og koordinaterne til krumningscirklens centrum:
\(f’(x) = \cos(x)\)
\(f’’(x) = \: – \sin(x)\)
\(R(x) = \dfrac{(1 + f’(x)^2)^{1,5}}{f’’(x)} = \: – \dfrac{(1 + \cos^2(x))^{1.5}}{\sin(x)}\), \(x\neq 0, \pi, 2\pi\)
\(\kappa(x) = \dfrac{1}{R(x)} = \: – \dfrac{\sin(x)}{(1 + \cos^2(x))^{1.5}}\)
\(x_C = x \:– \dfrac{1 + f’(x)^2}{f’’(x)}\cdot f’(x) = x + \dfrac{1 + \cos^2(x)}{\sin(x)}\cdot \cos(x)\)
\(= x + \dfrac{1 + \cos^2(x)}{\tan(x)}\), \(x\neq 0, \pi, 2\pi\)
\(y_C = f(x) + \dfrac{1 + f’(x)^2}{f’’(x)} = \sin(x)\: – \dfrac{1 + \cos^2(x)}{\sin(x)}\)
\(= \dfrac{\sin^2(x)\: – (\sin^2(x) + \cos^2(x))\: – \cos^2(x)}{\sin(x)} =\: – \dfrac{2\cos(x)}{\tan(x)}\), \(x\neq 0, \pi, 2\pi\)
I figur 5 er med blåt vist krumningscirklens centrums placering som funktion af x. Når x løber fra \(0^+\) til \(\pi^–\), krummer grafen nedad, og krumningscirklens centrum ligger her under grafen og vandrer fra det sydøstlige hjørne i koordinatsystemet op til x-aksen i \((\frac{\pi}{2},0)\) og videre til det sydvestlige hjørne i koordinatsystemet. Når x løber fra \(\pi^+\) til \(2\pi^–\), krummer grafen opad, og krumningscirklens centrum ligger her over grafen og vandrer fra det nordøstlige hjørne i koordinatsystemet ned til x-aksen i \((\frac{3\pi}{2},0)\) og videre til det nordvestlige hjørne i koordinatsystemet.
Når x er \(0, \pi\) og \(2\pi\) er krumningen \(0\), og her er hverken krumningsradius eller krumningscirklens centrum defineret. Ved disse x-værdier skifter krumning og krumningsradius fortegn, fordi \(f’’(x)\) skifter fortegn, og krumningscirklens centrum skifter mellem placering over og under grafen. I punkter, hvor \(f’’(x)\) skifter fortegn, siger vi, at grafen for \(f(x)\) har en vendetangent.
Vi ser, at krumningsradius er mindst (= 1,0) og krumningen er numerisk størst (= 1,0), når x er \(\frac{\pi}{2}\) og \(\frac{3\pi}{2}\). Krumningsradius er størst (uendelig stor), når x er tæt på \(0, \pi\) og \(2\pi\).
Videolektioner
I denne video giver vi en introduktion til begrebet krumning.
I denne video udleder vi formlen for beregning af krumning ud fra krumningscirklens radius.
