At rejse en normal i et punkt på en linje

Der er givet en linje (\(l\)) og et punkt (\(A\)) på linjen, som vist med blåt i figur 1. Vi skal rejse en normal til linjen \(l\) i punkt \(A\), dvs. konstruere en linje (\(n\)) der står vinkelret på linjen \(l\) og går gennem punkt \(A\).

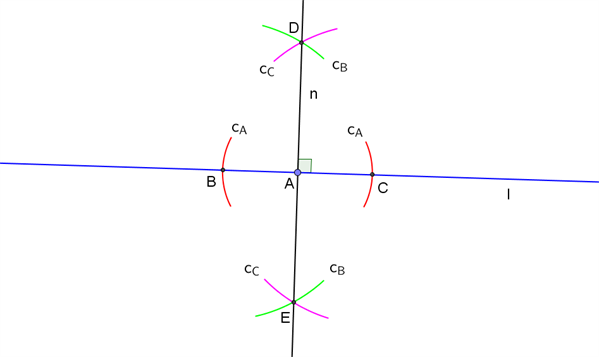
Figur 1          At rejse en normal

Fremgangsmåde, se figur 1:

1. tegn – med centrum i punkt \(A\)  – en cirkel (\(c_A\)) med en selvvalgt radius (i figur 1 er kun vist de to cirkelbuer (røde), der hører til cirklen \(c_A\), som skærer linjen \(l\)  hhv. til venstre og til højre for punkt \(A\))
2. de to skæringspunkter mellem linjen \(l\) og cirkelbuerne, der hører til cirklen \(c_A\), betegnes hhv. \(B\) (til  venstre for punkt \(A\)) og \(C\) (til højre for punkt \(A\))
3. tegn – med centrum i punkt \(B\) – en cirkel (\(c_B\)), der går gennem punkt \(C\) (i figur 1 er kun vist de to cirkelbuer (grønne) hørende til cirklen \(c_B\), som set i forhold til linjen \(l\) ligger hhv. ca. vinkelret over og ca. vinkelret under punkt \(A\))
4. tegn – med centrum i punkt \(C\) – en cirkel (\(c_C\)), der går gennem punkt \(B\) (i figur 1 er kun vist de to cirkelbuer (lyserøde) hørende til cirklen \(c_C\), som set i forhold til linjen \(l\) ligger hhv. ca. vinkelret over og ca. vinkelret under punkt \(A\))
5. de to skæringspunkter mellem cirkelbuerne hørende til cirklerne \(c_B\) og \(c_C\) betegnes hhv. \(D\) (over linjen \(l\)) og \(E\) (under linjen \(l\))
6. linjen gennem punkterne \(D\) og \(E\) er den ønskede normal (\(n\)), der står vinkelret på linjen \(l\) og går gennem punkt \(A\).