Polært koordinatsystem

Vi er vant til at arbejde i et retvinklet (x,y)-koordinatsystem – også kaldet et Cartesisk koordinatsystem – hvor punkter og vektorer beskrives ved den vandrette x-koordinat og den lodrette y-koordinat.

I nogle sammenhænge kan man med fordel istedet benytte et polært koordinatsystem, hvor punkter og vektorer beskrives med polære koordinater. Polære koordinater består dels af afstanden, angivet ved \(r\), fra polpunktet (svarende til Origo i et (x,y)-koordinatsystem) og dels af vinklen, angivet ved det græske bogstav theta \(\theta\), med den vandrette polarakse (svarende til den positive x-akse i et (x,y)-koordinatsystem), se figur 1.

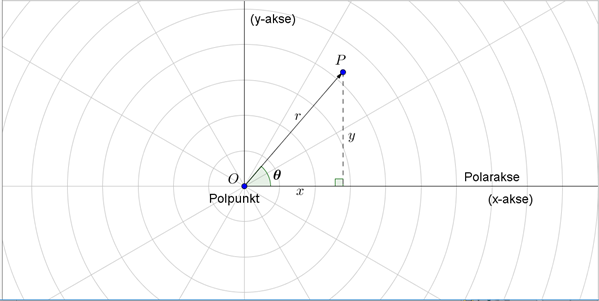
Figur 1          Polært koordinatsystem og sammenhæng med (x,y)-koordinatsystem

Et punkt \(P\) kan i et polært koordinatsystem beskrives ved stedvektoren \(\overrightarrow{OP}\) fra polpunktet \(O\) til punkt \(P\), og sammenhængen mellem \((r,\theta)\)-koordinaterne og (x,y)-koordinaterne er:

Polære koordinater	(x,y)-koordinater
\(r = \sqrt{x^2 + y^2}\)	\(x = r\cdot \cos{\theta}\)
\(\theta = \tan^{-1}(\frac{y}{x})\)	\(y = r\cdot \sin{\theta}\)

I et polært koordinatsystem angives funktioner som \(r(\theta)\), hvor vinklen, \(\theta\), er den uafhængige variabel, og afstanden, \(r\), er den afhængige variabel. 

Lad os se på et par eksempler, hvor polære koordinater med fordel kan benyttes, nemlig cirklen og en spiral, se figur 2.

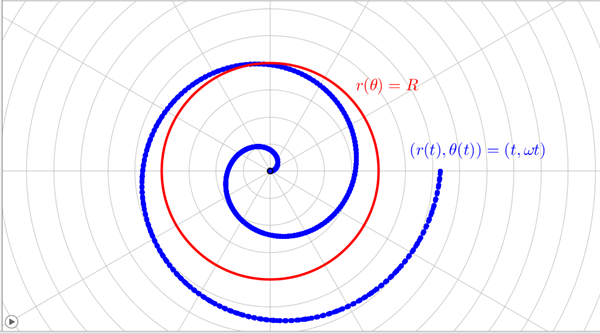
Figur 2          Cirklen og en spiral i et polært koordinatsystem

Ligningen for cirklen med centrum i Origo og radius \(R\) kender vi i et (x,y)-koordinatsystem som: \(x^2 + y^2 = R^2\). I et polært koordinatsystem bliver ligningen meget simplere, nemlig: \(r(\theta) = R\), vist med rødt i figur 2. Uanset størrelsen af vinklen \(\theta\) er afstanden fra polpunktet til cirkelperiferien lig med \(R\).

Et eksempel på en spiral i et (x,y)-koordinatsystem er givet ved parameterfremstillingen: \((x(t), y(t)) = (t\cdot\cos{\omega t}, t\cdot \sin{\omega t})\), hvor \(\omega = \frac{2\pi}{T}\) er vinkelhastigheden og \(T\) er tiden for en 360\(^\circ\) drejning. I et polært koordinatsystem bliver parameterfremstillingen noget simplere, nemlig: \((r(t),\theta(t)) = (t, \omega t)\), \(0\le t < \infty\), som vist med blåt i figur 2 for intervallet \(0\le t \le 2\cdot T\). 

Der er dog også mange eksempler på funktioner, hvor det polære koordinatsystem ikke er hensigtsmæssigt at bruge. Tænk eksempelvis på den rette linje, der skærer y-aksen i \(b\) og har hældningen \(a\). I et (x,y)-koordinatsystem kan denne linje beskrives ved den simple funktion: \(y = a\cdot x + b\). I et polært koordinatsystem bliver beskrivelsen noget mere kompliceret:

\(r(\theta) = |\dfrac{b}{\sin{\theta}\: –\: a\cdot \cos{\theta}}|\)

hvor \(|\: \:|\) angiver numerisk værdi og definitionsmængden for \(\theta\) er:
hvis \(b > 0\):        \(\tan^{-1}(a) < \theta < \tan^{-1}(a)\: +\: \pi\)
hvis \(b < 0\):        \(\tan^{-1}(a)\: –\: \pi < \theta < \tan^{-1}(a)\)

Ovenstående gælder kun, når \(b\ne 0\). Hvis \(b = 0\), går linjen gennem polpunktet og kan i polære koordinater beskrives som to halvlinier ved:

\(\theta = \tan^{-1}(a)\) og \(0 \le r < \infty\)
\(\theta = \tan^{-1}(a)\: +\: \pi\) og \(0 \le r < \infty\)

Når vi arbejder med funktioner givet ved polære koordinater, bliver integralregning forholdsvis simpelt at have med at gøre (ikke nødvendigvis udregning af integralet, men ihvertfald opstilling af integralet). Årsagen er, at infinitesimal-betragtningen med polære koordinater bliver en lille vinkeltilvækst, \(d\theta\), til vinklen \(\theta\), og vi har dermed at gøre med enten en infinitesimal cirkelbue, når vi skal beregne længden af en kurve, eller et infinitesimalt cirkeludsnit, når vi skal beregne areal. Begge dele giver simple regneudtryk, hvilket fremgår af de følgende par eksempler.

 

Eksempel 1

En lukket vejstrækning, som skal bruges til et cykelløb, er givet ved den polære funktion:

\(r(\theta) = 5\cdot \sqrt{3\cdot \cos^2(\theta)+1}, \: \: 0 \le \theta \le 2\pi\)

Enheden for \(r(\theta)\) er km. Vejstrækningen er vist i figur 3.

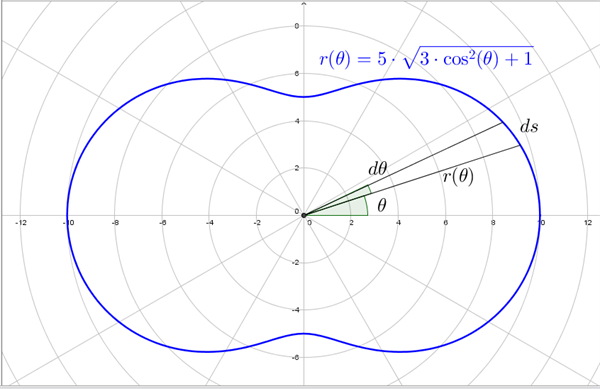
Figur 3          Vejstrækning til et cykelløb

Bestem længden af et cykelløb, hvor vejstrækningen givet ved \(r(\theta)\) gennemkøres 4 gange. Angiv længden i km med én decimals nøjagtighed.

I figur 3 betragter vi en lille vinkeltilvækst, \(d\theta\), til vinklen \(\theta\). Bidraget fra dette vinkeludsnit til omkredsen og dermed til vejstrækningens længde er en cirkelbue, bidraget er proportionalt med \(d\theta\) og kan beregnes som: \(ds = r(\theta) \cdot d\theta\). Hele omkredsen finder vi ved at integrere over definitionsområdet for \(\theta\):

\(O = \displaystyle \int_{start}^{slut} ds = \int_{0}^{2\pi} 5\cdot \sqrt{3\cdot \cos^2(\theta)+1}\cdot d\theta\)

Dette integral udregnes i CAS og giver en omkreds på \(O =\) 48,442 km. Når vejstrækningen skal gennemkøres 4 gange, er løbets længde: \(L = 4\cdot O =\) 193,8 km.

 

Eksempel 2

Et smykkevedhæng i sølv har form som givet ved den polære funktion:

\(r(\theta) = 4\cdot (2\cdot \cos(\theta)\: –\: \sin^2(\theta)),\: \: -1,14372 \le \theta \le 1,14372\)

Enheden for \(r(\theta)\) er cm. Formen er vist i figur 4.

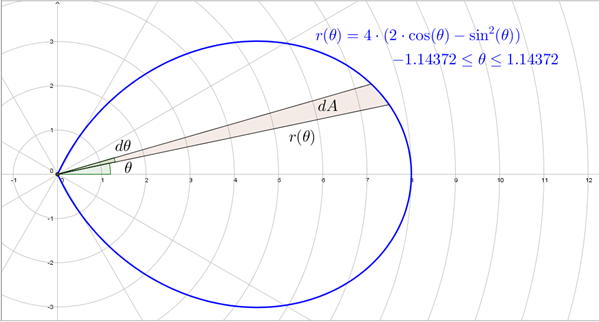
Figur 4          Formen på et smykkevedhæng

Bestem vægten af vedhænget, når vedhængets tykkelse, \(t\), er 2 mm og sølvets massefylde, \(\rho\), er 10 g/cm\(^3\).

Vi skal bestemme rumfanget af vedhænget og starter derfor med at bestemme arealet af formen i figur 4. Vi betragter en lille vinkeltilvækst, \(d\theta\), til vinklen \(\theta\). Bidraget fra dette vinkeludsnit til arealet er et cirkeludsnit, bidraget er proportionalt med \(d\theta\) og kan beregnes som: \(dA = \pi\cdot r(\theta)^2\cdot (\frac{d\theta}{2\pi}) = \frac{1}{2}\cdot r(\theta)^2\cdot d\theta\). Hele arealet finder vi ved at integrere over definitionsområdet for \(\theta\):

\(A = \displaystyle \int_{start}^{slut} dA = \int_{-1,14372}^{1,14372} \dfrac{1}{2}\cdot r(\theta)^2 \cdot d\theta\)
\(= \displaystyle \int_{-1,14372}^{1,14372} \dfrac{1}{2}\cdot 16\cdot (2\cdot \cos(\theta)\: –\: \sin^2(\theta))^2\cdot d\theta\)
\(= \displaystyle 32\cdot \int_{-1,14372}^{1,14372} (\cos^2(\theta)\: +\: \dfrac{1}{4}\cdot \sin^4(\theta)\: –\: \cos(\theta)\cdot \sin^2(\theta))\cdot d\theta\)

Dette integral udregnes i CAS og giver et areal på \(A =\) 11,5 cm\(^2\).

Rumfanget af vedhænget bestemmer vi ved at gange arealet med tykkelsen (i cm), og vægten af vedhænget bestemmer vi ved at gange rumfanget med massefylden:

\(M = V\cdot \rho = A\cdot t\cdot \rho = 11,5\cdot 0,2\cdot 10 = 23\)

Vedhængets vægt er altså 23 gram.