Logaritmisk skala på x-aksen

På samme måde som i det tidligere afsnit kan vi analysere spejlingen af punktområder i det sædvanlige (x,y)-koordinatsystem til en ny position i det enkelt-logaritmiske koordinatsystem med logaritmisk skala på x-aksen.

Vi bemærker igen, at logaritmen kun er defineret for positive parametre. Altså kan kun punkter med positiv x-værdi, dvs. 1. og 4. kvadrant i det sædvanlige (x,y)-koordinatsystem, spejles til punkter i dette enkelt-logaritmiske koordinatsystem.

Vi bemærker videre, at punktet P (1,0) i det sædvanlige (x,y)-koordinatsystem spejles over i Origo (0,0) i det enkelt-logaritmiske koordinatsystem, idet Log(x=1) = 0.

Hvis vi inddeler 1. og 4. kvadrant i det sædvanlige (x,y)-koordinatsystem i 4 områder (A₁, B₁, C₁, D₁) som vist øverst i figur 3, bliver disse spejlet over i de 4 kvadranter (A₂, B₂, C₂, D₂) i det enkelt-logaritmiske koordinatsystem, som vist nederst i figur 3:

(x.y)-koordinatsystem			Enkelt-logaritmisk koordinatsystem
A1:	x ≥ 1, y ≥ 0		A2:	Log(x) ≥ 0, y ≥ 0
B1:	0 < x ≤ 1, y ≥ 0		B2:	Log(x) ≤ 0, y ≥ 0
C1:	0 < x ≤ 1, y ≤ 0		C2:	Log(x) ≤ 0, y ≤ 0
D1:	x ≥ 1, y ≤ 0		D2:	Log(x) ≥ 0, y ≤ 0

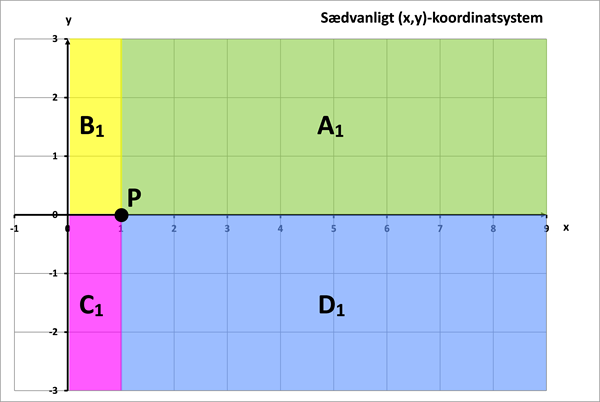
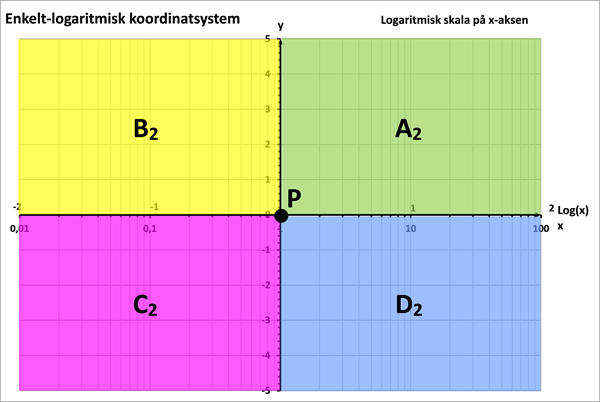
Figur 3         Spejling af punktområder i det sædvanlige (x,y)-koordinatsystem (øverst) til et enkelt-logaritmisk koordinatsystem med logaritmisk skala på x-aksen (nederst)

Punkter på y-aksen i det sædvanlige (x,y)-koordinatsystem er ikke med i hverken B₁ eller C₁, da disse punkter (med x-værdien 0) ikke kan spejles til dette enkelt-logaritmiske koordinatsystem.

For en god ordens skyld bemærker vi, at logaritmen til meget små, positive x-værdier, der kommer uendeligt tæt på nul, er store negative tal. Vi formulerer det matematisk som \(lim_{x\to 0^+} Log(x) = -\infty\).