Rumfang af omdrejnings-legeme drejet om y-aksen
Beregning af rumfang af omdrejningslegemer har du nok mødt tidligere, hvor x-aksen har været omdrejningsakse. Hvis ikke – eller hvis du vil genopfriske det – er her et link.
I dette afsnit vil vi kigge på omdrejningslegemer, hvor y-aksen er omdrejningsakse. I 1. kvadrant i et sædvanligt (x,y)-koordinatsystem er givet en funktion \(y = f(x)\), \(x_1\leq x\leq x_2\), og denne funktion roteres 360\(^\circ\) omkring y-aksen. Der fremkommer herved et rumligt omdrejningslegeme, se figur 1, og vi kunne være interesseret i at beregne dets rumfang.
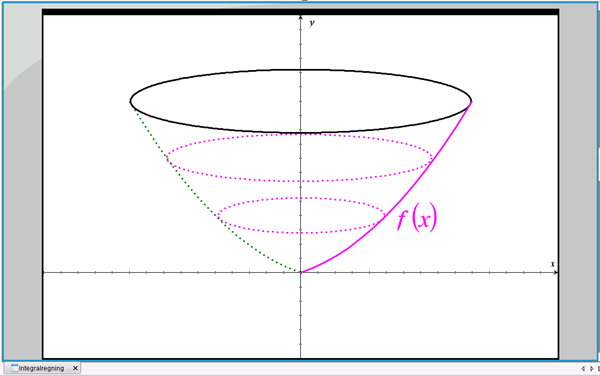
Figur 1 Rumligt legeme frembragt ved drejning af \(f(x)\) omkring y-aksen
Om funktionen \(f(x)\) vil vi i det aktuelle x-interval forlange, for det første at den er kontinuert, og for det andet at der for enhver y-værdi kun er én tilhørende x-værdi. Det kan oversættes til, at funktionens differentialkoefficient ikke må skifte fortegn, og dermed at henholdsvis største og mindste y-værdi skal forekomme i x-intervallets to endepunkter.
Figur 2 viser eksempler på funktioner, hvor dette ikke er opfyldt.
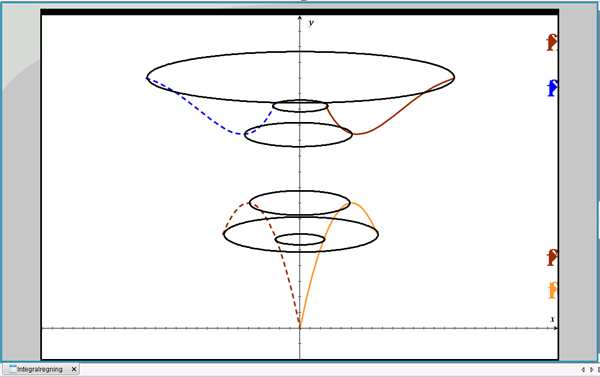
Figur 2 Funktioner, hvor hældningskoefficienten skifter fortegn i x-intervallet
Der fremkommer også her, som vi kan se, rumlige legemer ved drejning om y-aksen, men hvis vi skal beregne rumfanget af dem, vil vi være nødsaget til at foretage beregningen ad flere omgange.
Forestil dig, at vi skal beregne rumfanget af den øverste skål i figur 2. Først må vi finde rumfanget af den massive sokkel i midten, dvs. omdrejningslegemet hørende til den aftagende del af funktionen. Dernæst må vi finde rumfanget af omdrejningslegemet hørende til den voksende del af funktionen. Ved at trække disse to rumfang fra hinanden får vi skålens netto-rumfang.
Nu vender vi tilbage til skålen fra figur 1. For at komme frem til en formel for rumfanget, betragter vi en tynd skive af omdrejningslegemet ved en given y-værdi, se figur 3.
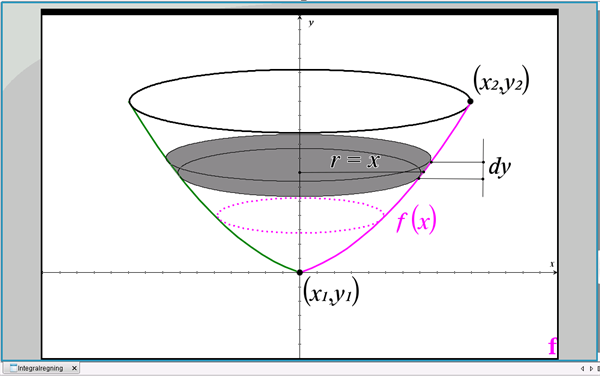
Figur 3 Bidrag til rumfang af omdrejningslegeme fra en infinitesimal skive
Skivens tykkelse er dy, og den har et cirkulært tværsnit med radius x. Skivens bidrag til rumfanget er derfor cirklens areal gange tykkelsen:
\(dV = (\pi\cdot r^2)\cdot dy = \pi\cdot x^2\cdot dy\)
I udtrykket indgår x sammen med dy, og derfor kan vi ikke umiddlebart integrere udtrykket. Vi må først enten omskrive x til en funktion af y eller omskrive dy til en funktion af dx.
I nogle tilfælde kan \(y = f(x)\) ved simpel omskrivning omformes til \(x = g(y)\), i andre tilfælde udnytter vi:
\(f’(x) = \dfrac{dy}{dx}\) og dermed \(dy = f’(x)\cdot dx\)
Ved indsætning i udtrykket for \(dV\) og integrering får vi nu to adgange til at beregne rumfanget:
Integral over y:
\(\displaystyle V = \int_{}^{} dV = \int_{y_1}^{y_2} \pi\cdot x^2\: dy = \int_{y_1}^{y_2} \pi\cdot g(y)^2\: dy\)
Integral over x:
\(\displaystyle V = \int_{}^{} dV = \int_{y_1}^{y_2} \pi\cdot x^2\: dy = \int_{x_1}^{x_2} \pi\cdot f’(x)\cdot x^2\: dx\)
hvor punkterne \((x_1, y_1)\) og \((x_2, y_2)\) er de to endepunkter på grafen for \(f(x)\).
Eksempel 1
I figur 4 er vist et vinglas.
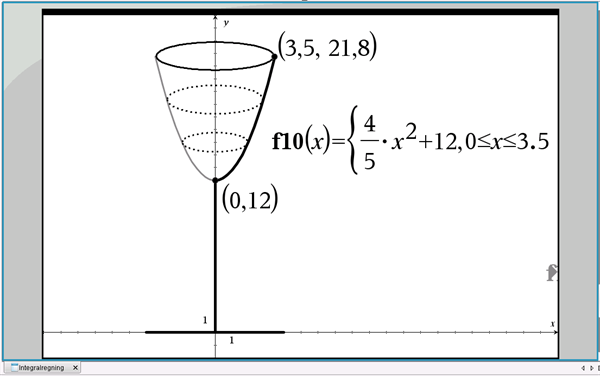
Figur 4 Vinglas stående på x-aksen
Foden står på x-aksen og stilken når op i højden 12 på y-aksen. Den indvendige kontur af vinglassets skål er givet ved funktionen \(y = f(x) = \frac{4}{5}x^2+12\), \(0\leq x\leq 3,5\), og vi beregner det tilhørende y-interval: \(12\leq y\leq 21,8\).
Vinglassets skål fremkommer ved at dreje \(f(x)\) 360\(^\circ\) om y-aksen, og vi skal bestemme skålens rumfang, idet alle mål er i cm.
Vi omskriver her funktionen \(y = f(x)\) til \(x = g(y) = \sqrt{\frac{5}{4}\cdot (y-12)}\) og benytter integralet med integration over y. \(g(y)\) indsættes og rumfanget bestemmes:
\(\displaystyle V = \int_{y_1}^{y_2} \pi\cdot g(y)^2\: dy = \int_{12}^{21,8} \pi\cdot \dfrac{5}{4}\cdot (y-12)\: dy \\ \displaystyle = \dfrac{5}{4}\cdot\pi\cdot \Big[\dfrac{1}{2}y^2 - 12y\Big]_{12}^{21,8} \\ \displaystyle = \dfrac{5}{4}\cdot\pi\cdot\big\{(\dfrac{1}{2}\cdot 21,8^2 - 12\cdot 21,8) - (\dfrac{1}{2}\cdot 12^2 - 12\cdot 12)\big\}\)
\(\displaystyle V = 189\) cm3 \(= 0,189\) liter
Vinglasset kan altså rumme lidt under en femtedel liter.
Eksempel 2
I figur 5 er vist en isvaffel. Isvaflens bund er i -15 på y-aksen, og isvaflens overside flugter med x-aksen og har en diameter på 8.
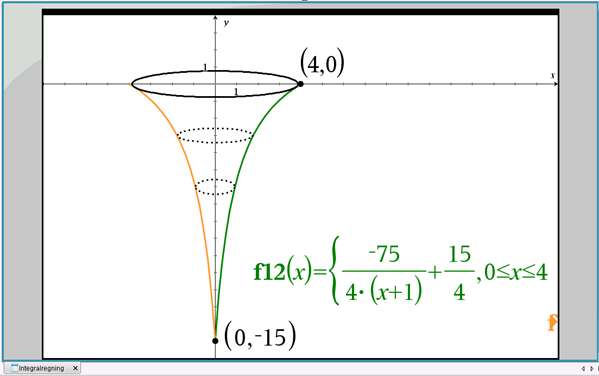
Figur 5 Isvaffel
Den indvendige kontur af isvaflen er givet ved funktionen \(y = f(x) = \dfrac{-75}{4\cdot (x+1)}+\dfrac{15}{4}\), \(0\leq x\leq 4\), og isvaflens inderside fremkommer ved at dreje \(f(x)\) 360\(^\circ\) om y-aksen.
Vi skal bestemme isvaflens rumfang, idet alle mål er i cm.
Vi differentierer: \(f'(x) = \dfrac{75}{4\cdot (x+1)^2}\), og vi benytter integralet med integration over x. \(f’(x)\) indsættes og rumfanget bestemmes:
\(\displaystyle V = \int_{}^{} dV = \int_{x_1}^{x_2} \pi\cdot f’(x)\cdot x^2\: dx = \int_{0}^{4}\pi\cdot\dfrac{75}{4}\cdot\dfrac{x^2}{(x+1)^2}\: dx \\ \displaystyle = \dfrac{75}{4}\cdot\pi\cdot\int_{0}^{4}\dfrac{x^2+2x+1}{(x+1)^2} + \dfrac{2-1}{(x+1)^2} - \dfrac{2x+2}{(x+1)^2}\: dx\)
Omskrivningen til tre brøker under integraltegnet giver os mulighed for at løse opgaven analytisk:
\(\displaystyle V = \dfrac{75}{4}\cdot\pi\cdot\Big\{\int_{0}^{4}1+(x+1)^{-2}\: dx - \int_{1}^{25}\dfrac{1}{z}\: dz\Big\}\)
idet vi til det sidste integral har benyttet substitutionen: \(z = (x+1)^2\), \(dz = (2x+2)\cdot dx\) samt \(z_1 = (0+1)^2 = 1\) og \(z_2 = (4+1)^2 = 25\). Vi får:
\(\displaystyle V = \dfrac{75}{4}\cdot\pi\cdot\Big\{\Big[x - \dfrac{1}{x+1}\Big]_0^4 - \big[ln(z)\big]_1^{25}\Big\} \\ = \dfrac{75}{4}\cdot\pi\cdot\big\{(4 - \dfrac{1}{5}) - (0 - 1) - (ln(25) - \ln(1))\big\} \\ = \dfrac{75}{4}\cdot\pi\cdot\big\{5 - \dfrac{1}{5} – 2\cdot \ln(5)\big\}\)
\(\displaystyle V = 93\) cm3 \(= 0,093\) liter
I udregningen har vi benyttet regnereglen for logaritmen af et kvadrattal: her \(\ln(25) = \ln(5^2) = 2\cdot \ln(5)\) og at \(\ln(1)=0\).
Isvaflen kan altså rumme lidt under en tiendedel liter, men heri er selvfølgelig ikke indregnet, at der kan fyldes is eller softice langt op over vaflens kant.
