Trigonometriske grundligninger

Fortegn på \( \cos , \sin \) og \( \tan \)

Før vi begynder at diskutere løsninger til såkaldte trigonometriske grundligninger, ser vi lidt på fortegnene for de forskellige trigonometriske funktioner. For \( \cos \) og \( \sin \) handler det om at undersøge, om \( x- \) og \( y \)-værdien til et givet punkt er positivt, idet \( \cos \) er defineret som \( x \)-værdien til et punkt til enhedscirklen, mens \( \sin \) er \( y \)-værdien. Fortegnene er illustreret i figuren nedenfor.

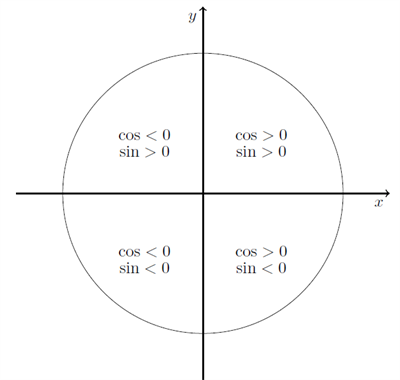
Når vi skal bestemme fortegnene for tangens, skal vi tænke os lidt mere om. Husk, at tangens er defineret som

$$ \tan (v) =  \frac{\sin(v)}{\cos(v)}.$$

Da vi ikke må dividere med \( 0 \), kan fortegnene for tangens bestemmes ved hjælp af fortegnene for sinus og cosinus, så længe cosinus ikke er \( 0 \), som er ved \( \pm \frac{\pi}{2} \).

Hvis cosinus og sinus begge er positive, bliver tangens også positiv, da vi dividerer to positive tal. Ligeledes bliver tangens også positiv, hvis både cosinus og sinus er negative, da vi kan gange både tæller og nævner med \( - 1 \), så vi kommer tilbage til en brøk med positiv tæller og nævner. Hvis enten cosinus eller sinus er negativ, mens den anden er positiv, får vi at tangens er negativ (se regneregler for negative tal). Det giver fortegnene illustreret i figuren nedenfor.

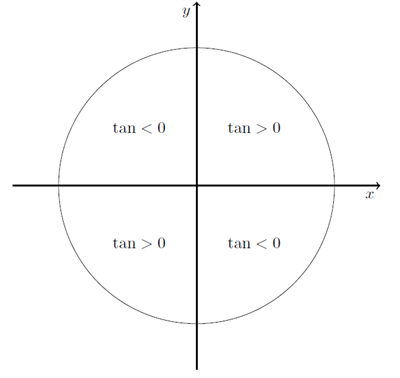
Trigonometriske grundligninger

Trigonometriske grundligninger er ligninger på formen 

$$\cos(v) = k \\
\sin(v) = k \\
\tan(v) = k$$

Lad os starte med at overveje, hvilke værdier af \( k \), der kan have en løsning. Da cosinus og sinus udgør henholdsvis \( x \)- og \( y \)-koordinaten for punkter på enhedscirklen. Alle punkterne på enhedscirklen har både \( x \)- og \( y \)-værdier mellem \( -1 \) og \( 1 \), så der er kun løsninger til \( \cos(v) = k \) og \( \sin(v) = k \), hvis

$$ -1 \leq k \leq 1. $$

Tilfældet er lidt mere kompliceret for tangens, da det er en brøk på formen

$$ \tan(v) = \frac{ \sin(v) }{ \cos(v) }. $$

Lidt viften med hænderne: Hvis \( \cos(v) \) bliver meget, meget lille, bliver \( \tan(v) \) meget, meget stor. På denne måde kan man finde vinkler, så \( \tan(v) = k \) for ethvert reelt tal \( k \). 

Hvordan løser man det så?

Cosinus:

Lad os illustrere det ved hjælp af eksempler. For cosinus skal vi huske på, at det er \( x \)-værdien for punkterne på enhedscirklen. Det vil sige, at hvis vi skal løse den trigonometriske grundligning

$$ \cos (v) = 0,3 $$

skal vi finde de punkter på enhedscirklen, der har \( x \)-værdi lig \( 0,3 \). Nedenfor er skitseret en metode til at løse sådan en ligning:

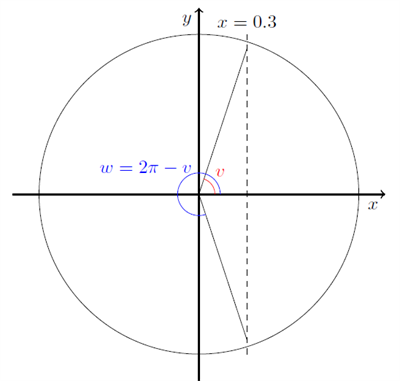
Metoden kan beskrives som en 3-trins raket:

1. Da vi er på jagt efter \( x \)-værdier (vi arbejder med cosinus), tegn en linje ved \( x = k \), her er tegnet en stiplet linje ved \( x = 0,3 \). 
2. Identificér en vinkel, så cosinus til den vinkel har den ønskede \( x \)-værdi. Her har vi tegnet vinklen \( v \) ved at forbinde origo, \( (0;0) \), med skæringspunktet mellem cirklen og den stiplede linje. Vi måler vinklen til ca. \( 72 ^\circ\)  eller 1,26 radianer
3. For at finde den anden vinkel, tager vi \( w = 2 \pi - v = 5,01 \) radianer.

De \( 2 \pi \) kommer fra, at vinklen, der går ned under \( x \)-asken ud til den stiplede linje, er lige så stor som \( v \), men med modsat fortegn. Det vil sige, vi skal hele vejen rundt i cirklen, bortset fra de sidste \( v \) radianer.

Sinus

Vi gentager 3-trinsraketten. Vi vil nu løse ligningen 

$$ \sin(v) = 0,3 $$

Illustrationen er givet nedenfor:

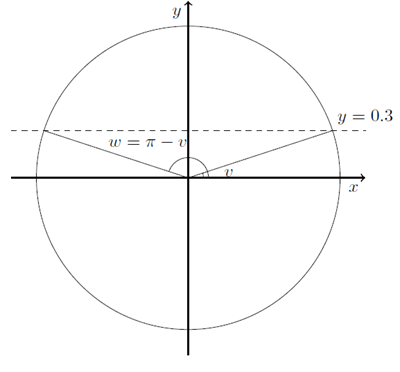
1. Da vi er på jagt efter \( y \)-værdier (vi arbejder med sinus), tegn en linje ved \( y = k \), her er tegnet en stiplet linje ved \( y = 0,3 \). 
2. Identificer en vinkel, så sinus til den vinkel har den ønskede \( y \)-værdi. Her har vi tegnet vinklen \( v \) ved at forbinde origo, \( (0;0) \), med skæringspunktet mellem cirklen og den stiplede linje. Vi måler vinklen til ca. \( 19 ^\circ\) eller 0,33 radianer
3. For at finde den anden vinkel, tager vi \( w = \pi - v = 2,81 \) radianer.

\( \pi \) kommer fra, at den vinklen \( v \) er spejlet i \( y \)-aksen, så vi skal gå halvvejs rundt i cirklen, \( \pi \), bortset fra en vinkel \( v \).

Tangens

Lad os nu sige, at vi vil løse grundligningen \( \tan(v) = k \). Som diskuteret før, kan denne ligning løses for et hvert reelt tal, \( k \). 

Husk, at den geometriske fortolkning af tangens er som beskrevet i figuren nedenfor (se afsnit om tangens).

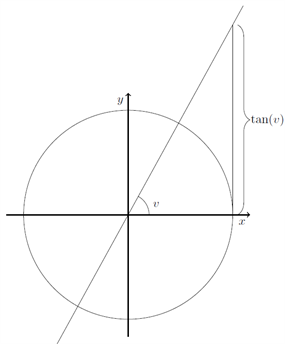
Vi indtegner en vinkel \( v \). Derefter tegner vi en tangent til cirklen i punktet \( (1,0) \) og ser, hvor vinklen skærer denne linje. Tangens til vinklen er defineret som \( y \)-værdien til dette skæringspunkt.

Lad os nu sige, vi skal løse ligningen \( \tan(v) = 1,7 \). Vi løser denne, som vi løste ligningerne for cosinus og sinus.

1. Tegn et linjestykke, der ligger som linjestykket \( \tan(v) \) i figuren ovenfor. Linjestykket skal have længde \( 1,7 \). 
2. Tegn en linje fra origo, \( (0;0) \), ud til enden af linjestykket med længde \( 1,7 \)
3. Mål vinklen. Her måler vi vinklen til \( v = 1,08 \) radianer. De to løsninger til \( \tan(v) = 1,7 \) er \( v \) og \( v + \pi \).