Arealet af trekanten
En trekant er karakteriseret ved de tre sidelængder \(a\), \(b\) og \(c\) og de tilhørende modstående vinkler \(A\), \(B\) og \(C\), se figur 1.
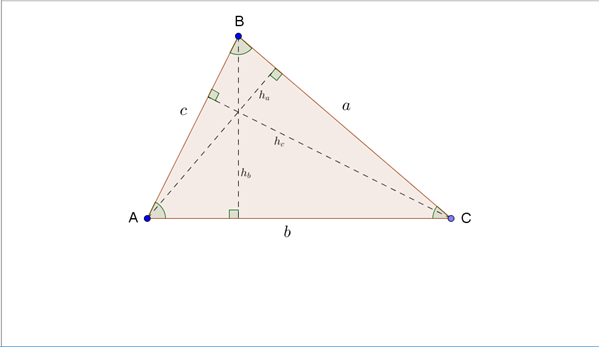
Figur 1 Trekanten med dens tre højder indtegnet
Fra barnsben har vi lært, at arealet af trekanten kan bestemmes vha. en grundlinje og en højde i trekanten (vi kan vilkårligt vælge siden a, b eller c som grundlinje sammen med den tilhørende højde):
\(A_{trekant}= \dfrac{1}{2}\cdot h\cdot g = \dfrac{1}{2}\cdot h_a\cdot a = \dfrac{1}{2}\cdot h_b\cdot b = \dfrac{1}{2}\cdot h_c\cdot c\)
Af de grundlæggende trigonometriske regneregler ses af figur 1, at højderne i trekanten kan bestemmes ud fra en sidelængde og sinus til en vinkel, derfor kan arealet af trekanten også bestemmes vha. to sider og den mellemliggende vinkel (vi kan vilkårligt vælge vinkel A, B eller C som den mellemliggende vinkel sammen med de to tilhørende sider):
\(A_{trekant} = \dfrac{1}{2}\cdot b\cdot c\cdot \sin{A} = \dfrac{1}{2}\cdot a\cdot c\cdot \sin{B} = \dfrac{1}{2}\cdot a\cdot b\cdot \sin{C}\)
Den omskrevne cirkel
I en vilkårlig trekant kan vi indtegne de tre siders midtnormaler, se figur 2. En sides midtnormal står vinkelret på siden og deler den i to lige store dele. Midtnormalerne har et fælles skæringspunkt, \(P\), som er centrum for den omskrevne cirkel, der går gennem de tre vinkelspidser.
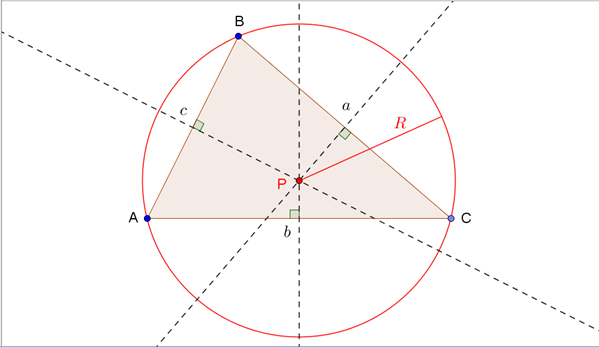
Figur 2 Trekanten med dens tre midtnormaler og den omskrevne cirkel indtegnet
Den omskrevne cirkels radius betegnes \(R\), og der gælder følgende sammenhæng mellem trekantens areal og \(R\), hvilket samtidig giver os en ligning til bestemmelse af \(R\), hvis vi kender arealet via en af de øvrige arealformler:
\(A = \dfrac{a\cdot b\cdot c}{4\cdot R} \implies R = \dfrac{a\cdot b\cdot c}{4\cdot A}\)
Bevis:
Vi forestiller os et koordinatsystem lagt henover trekanten i figur 3 med Origo i punkt \(A\) og x-aksen sammenfaldende med \(AC\). Trekantens vinkelspidser og den omskrevne cirkels centrum har da koordinaterne:
\(A = (0, 0), B = (x_B, y_B), C = (b, 0), P = (x_P, y_P)\)
Afstanden fra \(A\) til \(P\) er radius i den omskrevne cirkel, så \(x_P^2 + y_P^2 = R^2\), og da \(|AB| = c\), er \(x_B^2 + y_B^2 = c^2\). Vi kan opstille følgende udtryk for kvadratet på afstanden fra \(B\) til \(P\):
\(|BP|^2 = (x_P - x_B)^2 + (y_P - y_B)^2\)
\(= (x_P^2 + y_P^2) + (x_B^2 + y_B)^2 - 2x_Bx_P - 2y_By_P\)
\(= R^2 + c^2 - 2x_Bx_P - 2y_By_P = R^2\)
Da punkt \(P\) ligger på midtnormalen til siden \(b\), er \(x_P = \frac{b}{2}\), hvilket vi indsætter ovenfor og får:
\(y_P = \dfrac{c^2 - b\cdot x_B}{2\cdot y_B}\)
Vi indsætter nu udtrykkene for \(x_P\) og \(y_P\) i afstandsformlen for \(|AP|\):
\(|AP|^2 = R^2 = x_P^2 + y_P^2 = \dfrac{1}{4}\cdot b^2 + \dfrac{c^4 + b^2\cdot x_B^2 -\: 2\cdot b\cdot c^2\cdot x_B}{4\cdot y_B^2}\)
Vi sætter på fælles brøkstreg og udnytter, at \(x_B^2 + y_B^2 = c^2\), \(y_B = c\cdot \sin{A}\) og \(x_B = c\cdot \cos{A}\):
\(R^2 = \dfrac{b^2\cdot y_B^2 + c^4 + b^2\cdot x_B^2 -\: 2\cdot b\cdot c^2\cdot x_B}{4\cdot y_B^2} = \dfrac{b^2 + c^2 - 2\cdot b\cdot c\cdot \cos{A}}{4\cdot \sin^2{A}}\)
Vi genkender tælleren på højresiden som cosinus-relationen til bestemmelse af sidelængden \(a^2\) og udnytter afslutningsvis, at \(A = \frac{1}{2}\cdot b\cdot c\cdot \sin{A}\) og dermed at \(\sin{A} = \frac{2\: \cdot \:A}{b\: \cdot \:c}\), hvilket fører os frem til:
\(R^2 = \dfrac{a^2}{4\cdot \sin^2{A}} = \dfrac{a^2\cdot b^2\cdot c^2}{16\cdot A^2} \implies A = \dfrac{a\cdot b\cdot c}{4\cdot R}\)
Hermed er arealformlen vha. den omskrevne cirkels radius bevist.
Videolektion
I denne videolektion bliver beviset for arealformlen vha. den omskrevne cirkels radius gennemgået.
Den indskrevne cirkel
I en vilkårlig trekant kan vi indtegne de tre vinklers vinkelhalveringslinjer, se figur 3. Vinkelhalveringslinjerne har et fælles skæringspunkt, \(Q\), som er centrum for den indskrevne cirkel, der netop tangerer alle tre sider i trekanten.
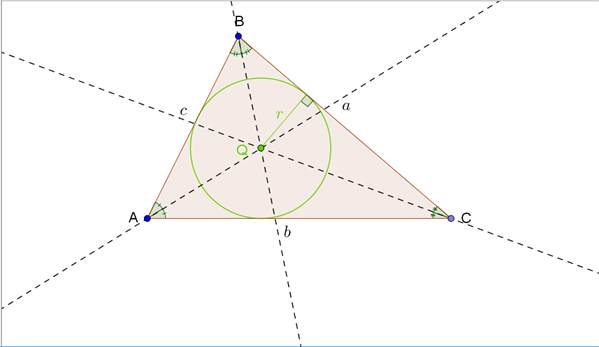
Figur 3 Trekanten med dens tre vinkelhalveringslinjer og den indskrevne cirkel indtegnet
Den indskrevne cirkels radius betegnes \(r\), og der gælder følgende sammenhæng mellem trekantens areal og \(r\), hvilket samtidig giver os en ligning til bestemmelse af \(r\), hvis vi kender arealet via en af de øvrige arealformler:
\(A = r\cdot s \implies r = \dfrac{A}{s}\), hvor \(s = \frac{1}{2}\cdot (a + b + c)\)
Hjælpestørrelsen \(s\) er lig med halvdelen af trekantens omkreds.
Bevis:
I figur 3 kan trekant \(ABC\) opdeles i tre mindre trekanter: \(ABQ\), \(BCQ\) og \(AQC\), som hver har en af trekant \(ABC\)'s sidelængder som grundlinje. Da alle tre sider i trekant \(ABC\) er tangent til den indskrevne cirkel, er højden i hver af de små trekanter = den indskrevne cirkels radius \(r\), så:
\(A_{ABC} = A_{ABQ} + A_{BCQ} + A_{AQC} = \frac{1}{2}\cdot c\cdot r + \frac{1}{2}\cdot a\cdot r + \frac{1}{2}\cdot b\cdot r\)
\(= \frac{1}{2}\cdot (a+b+c)\cdot r = r\cdot s\)
Hermed er arealformlen vha. den indskrevne cirkels radius bevist.
Videolektion
I denne videolektion bliver beviset for arealformlen vha. den indskrevne cirkels radius gennemgået.
Herons formel
Trekantens areal kan også bestemmes vha. Herons formel, opkaldt efter den græske matematiker Heron:
\(A = \sqrt{s\cdot (s-a)\cdot (s-b)\cdot (s-c)}\), hvor \(s = \frac{1}{2}\cdot (a + b + c)\)
Hjælpestørrelsen \(s\) er lig med halvdelen af trekantens omkreds.
Bevis:
Vi tager udgangspunkt i, at trekantens areal kan bestemmes vha. siden \(b\) og højden \(h_b\):
\(A = \frac{1}{2}\cdot b\cdot h_b = \frac{1}{2}\cdot a\cdot b\cdot \sin{C}\)
Vi opløfter til anden potens på begge sider:
\(A^2 = \frac{1}{4}\cdot a^2\cdot b^2\cdot \sin^2{C} = \frac{1}{4}\cdot a^2\cdot b^2\cdot (1 - \cos^2{C})\)
Her indsætter vi cosinus-relationen for \(\angle C\): \(\cos{C} = \frac{a^2 +\: b^2 -\: c^2}{2ab}\):
\(A^2 = \frac{1}{4}\cdot a^2\cdot b^2\cdot (1 - \frac{(a^2 +\: b^2 -\: c^2)^2}{4a^2b^2}) = \frac{1}{4}\cdot a^2\cdot b^2\cdot \frac{4a^2b^2 -\: (a^2 +\: b^2 -\: c^2)^2}{4a^2b^2}\)
\(= \frac{1}{16}\cdot (4a^2b^2 - (a^4 + b^4 + c^4 + 2a^2b^2 - 2a^2c^2 - 2b^2c^2))\)
\(= \frac{1}{16}\cdot (2a^2b^2 + 2a^2c^2 + 2b^2c^2- (a^4 + b^4 + c^4 ))\)
Vi gætter på, at højresiden kan omskrives til: \(s\cdot (s-a)\cdot (s-b)\cdot (s-c)\), hvor \(s\) er den halve omkreds: \(s = \frac{1}{2}\cdot (a+b+c)\):
\(s\cdot (s - a)\cdot (s - b)\cdot (s - c)\)
\(= \frac{1}{2}\cdot (a + b + c)\cdot \frac{1}{2}\cdot (b + c - a)\cdot \frac{1}{2}\cdot (a + c - b)\cdot \frac{1}{2}\cdot (a + b - c)\)
\(= \frac{1}{16}\cdot (ab + ac - a^2 + b^2 + bc - ab + bc + c^2 - ac)\)
\(\cdot\: (a^2 + ab - ac + ac + bc - c^2 - ab - b^2 + bc)\)
\(= \frac{1}{16}\cdot (-a^2 + 2bc + b^2 + c^2)\cdot (a^2 + 2bc - b^2 - c^2)\)
\(= \frac{1}{16}\cdot (-a^4 - 2a^2bc + a^2b^2 + a^2c^2 + 2a^2bc + 4b^2c^2 - 2b^3c - 2bc^3\)
\(+\: a^2b^2 +2b^3c - b^4 - b^2c^2 +a^2c^2 + 2bc^3 - b^2c^2 - c^4 )\)
\(= \frac{1}{16}\cdot (2a^2b^2 + 2a^2c^2 + 2b^2c^2- (a^4 + b^4 + c^4 ))\)
Det var et godt gæt (!), og vi har hermed bevist Herons formel:
\(A^2 = s\cdot (s-a)\cdot (s-b)\cdot (s-c) \implies A = \sqrt{s\cdot (s-a)\cdot (s-b)\cdot (s-c)}\)
Videolektion
I denne videolektion bliver beviset for Herons formel gennemgået.
Eksempler
Vi ser på to eksempler på brugen af formlerne.
Eksempel på arealbestemmelse vha. to sidelængder og den mellemliggende vinkel:
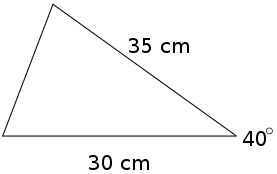
Her kender vi to sidelængder og den mellemliggende vinkel, og derfor beregner vi arealet ved:
\(A = \dfrac{1}{2}\cdot a\cdot b\cdot \sin{C}\)
Længden a er 35 cm, længden b er 30 cm og vinklen er \(40^\circ\):
\(A = \dfrac{1}{2}\cdot 30\cdot 35\cdot \sin{40^\circ} = 337,5\: cm^2\)
Eksempel på arealbestemmelse vha. den omskrevne cirkel:
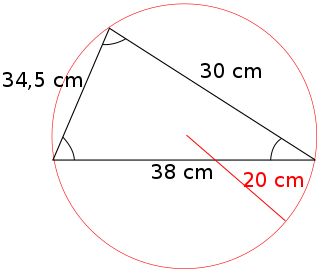
Her kan arealet af trekanten beregnes med den omskrevne cirkel:
\(A = \dfrac{a\cdot b\cdot c}{4\cdot R}\)
\(A = \dfrac{30\cdot 38\cdot 34,5}{4\cdot 20} = 491,6\: cm^2\)
