Pilhøjde
For både cirkeludsnittet og cirkelbuen fastlægges korden, \(k\), som linjestykket, der forbinder cirkelbuens to endepunkter. Vinkelhalveringslinjen for cirkeludsnittet/cirkelbuen er samtidig midtnormal til korden, \(k\), dvs. den står vinkelret på korden og deler den i to lige store dele, se figur 4.
Pilhøjden defineres som afstanden – målt langs vinkelhalveringslinjen – fra korden, \(k\), til cirkelperiferien.
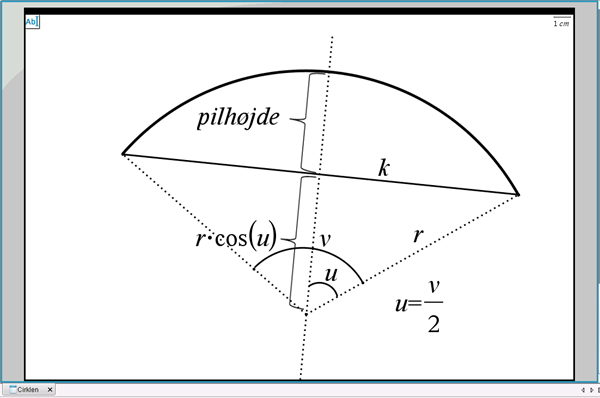
Figur 4 Pilhøjde for et cirkeludsnit/en cirkelbue
Det ses af figuren, at pilhøjden er givet ved \( r – r\cdot\cos(\frac{v}{2}) = r\cdot (1-\cos(\frac{v}{2}))\),
hvor \(0<v\leq 180^\circ\) eller \(0<v\leq\pi\)
Nogle taleksempler:
| \(v\) (grader) | \(v\) (radianer) | Pilhøjde |
| \(30^\circ\) | \(\frac{\pi}{6}\) | \(r\cdot (1-\cos(15^\circ)) = 0{,}034\cdot r\) |
| \(45^\circ\) | \(\frac{\pi}{4}\) | \(r\cdot (1-\cos(22,5^\circ)) = 0{,}076\cdot r\) |
| \(60^\circ\) | \(\frac{\pi}{3}\) | \(r\cdot (1-\cos(30^\circ)) = r\cdot \big(1-\frac{\sqrt{3}}{2}\big) = 0{,}134\cdot r\) |
| \(90^\circ\) | \(\frac{\pi}{2}\) | \(r\cdot (1-\cos(45^\circ)) = r\cdot \big(1-\frac{\sqrt{2}}{2}\big) = 0{,}293\cdot r\) |
| \(120^\circ\) | \(\frac{2\pi}{3}\) | \(r\cdot (1-\cos(60^\circ)) = r\cdot \big(1-\frac{1}{2}\big) = 0{,}5\cdot r\) |
| \(135^\circ\) | \(\frac{3\pi}{4}\) | \(r\cdot (1-\cos(67,5^\circ)) = 0{,}617\cdot r\) |
| \(150^\circ\) | \(\frac{5\pi}{6}\) | \(r\cdot (1-\cos(75^\circ)) = 0{,}741\cdot r\) |
| \(180^\circ\) | \(\pi\) | \(r\cdot (1-\cos(90^\circ)) = r\cdot (1-0) = r\) |
Området mellem cirkelbuen og korden, \(k\), betegner vi \(M\), se figur 5.
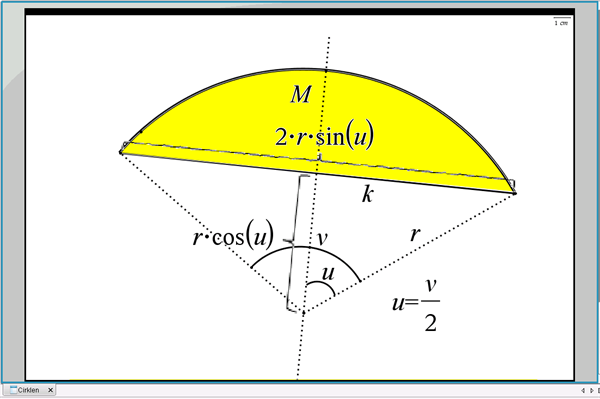
Figur 5 Areal af område mellem cirkelbue og korde
Arealet af \(M\) kan beregnes som arealet af hele cirkeludsnittet hørende til cirkelbuen fratrukket arealet af trekanten under korden, \(k\). I trekanten under korden, \(k\), er grundlinjen \(g = 2\cdot r\cdot\sin(\frac{v}{2})\) og højden \(h = r\cdot\cos(\frac{v}{2})\), og dermed er arealet af trekanten under korden:
\(A_k = \dfrac{1}{2}\cdot g\cdot h = r^2\cdot\sin(\frac{v}{2})\cdot\cos(\frac{v}{2})\).
Hvis vinklen, v, angives i grader (\(0<v\leq 180^\circ\)), er arealet af \(M\) :
\(A_M = A_{udsnit} – A_k = \dfrac{v}{360}\cdot\pi\cdot r^2 – r^2\cdot\sin(\frac{v}{2})\cdot\cos(\frac{v}{2})\)
\(= \pi\cdot r^2\cdot (\dfrac{v}{360} - \dfrac{1}{\pi}\cdot \sin(\frac{v}{2})\cdot \cos(\frac{v}{2}))\)
Hvis vinklen, v, angives i radianer (\(0<v\leq\pi\)), er arealet af \(M\):
\(A_M = A_{udsnit} – A_k = \dfrac{v}{2}\cdot r^2 - r^2\cdot\sin(\frac{v}{2})\cdot\cos(\frac{v}{2})\)
\(= r^2\cdot (\dfrac{v}{2}-\sin(\frac{v}{2})\cdot\cos(\frac{v}{2}))\)
Alternativ formel
Hvis man gerne vil undgå cosinus og sinus, kan følgende formel også bruges til at bestemme pilhøjden:
$$ r = \frac{k^2}{8h}+\frac{h}{2} $$
Idet vi ved, at pilhøjden altid har en værdi mellem 0 og radius r, og at \( r \geq \frac{k}{2}\)kan vi få følgende udtryk:
$$ h = r- \sqrt{r^2-\bigg(\frac{k}{2}\bigg)^2} $$
