Differentiation af funktionen f(x) = log$_{10}$(x)

Sammenhængen mellem 10-tals logaritmen og den naturlige logaritme er:

$f(x) = \log_{10}(x) = \dfrac{1}{\ln(10)}\cdot \ln(x), x>0$

Vi ser, at 10-tals logaritmen er lig med den naturlige logaritme multipliceret med et tal (den reciprokke værdi af $\ln(10)$), og differentialkvotienten for 10-tals logaritmen er dermed lig med differentialkvotienten for den naturlige logaritme divideret med den naturlige logaritme til 10.

Da differentialkvotienten for den naturlige logaritme er $\frac{1}{x}$, når vi frem til:

$f(x) = \log_{10}(x) \implies f’(x) = \dfrac{1}{\ln(10)}\cdot \dfrac{1}{x} = \dfrac{1}{x\cdot \ln(10)} = \dfrac{\frac{1}{x}}{\ln(10)}, x>0$

Overalt på grafen for 10-tals logaritmen, se figuren, kan vi altså beregne grafens hældning og dermed tangentens hældning som den reciprokke værdi af x divideret med $\ln(10)\approx 2,30$.

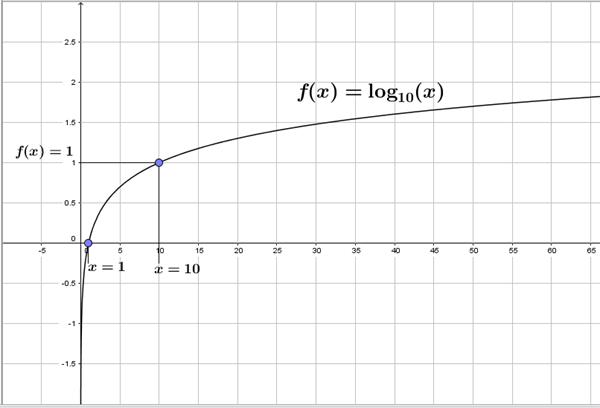
Figur          Grafen for $f(x) = \log_{10}(x)$