Bestem forskriften for et andengradspolynomium ud fra toppunktet og to punkter på grafen

Parablens toppunkt er på y-aksen i $y_T$, og vi får derudover oplyst y-værdien, $y_1$, i to punkter beliggende symmetrisk omkring toppunktet, i hhv. $+ x_1$ og $- x_1$, se figur 1.

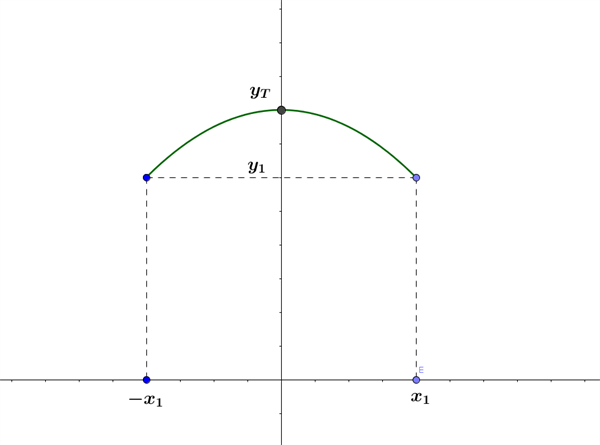
Figur 1          Parabel med toppunkt på y-aksen og to symmetriske punkter kendt

Vi tager udgangspunkt i den generelle form for forskriften for et andengrads­polynomium: $y(x)=a\cdot x^2 + b\cdot x + c$:

• vi ved, at tallet $c$ i forskriften angiver skæring med y-aksen – så vi kan direkte på grafen aflæse tallet $c = y_T$
• vi ved, at x-koordinaten for parablens toppunkt er givet ved: $x_T = \frac{-b}{2a}$. Da toppunktet ligger på y-aksen (hvor x-koordinaten er 0), kan vi konkludere, at tallet $b = 0$
• vi kan heraf udlede: $y(x_1) = y(- x_1) = a\cdot {x_1}^2 + 0\cdot x_1 + c = a\cdot {x_1}^2 + y_T = y_1$, som giver os en ligning til bestemmelse af $a$: 

$a=\dfrac{y_1-y_T}{x_1^2}$

• og forskriften for andengrads­polynomiet er dermed:

$y(x)=\dfrac{y_1-y_T}{x_1^2}\cdot x^2+y_T$

Hvis $y_1 > y_T$ er parablen glad, og hvis $y_T > y_1$ er parablen sur.

Videolektion

Eksempel

For en bro, der til forveksling ligner Dronning Alexandrines Bro (også kaldet Mønbroen, se foto), er i figur 2 vist et tværsnit af gennemsejlingsfaget.

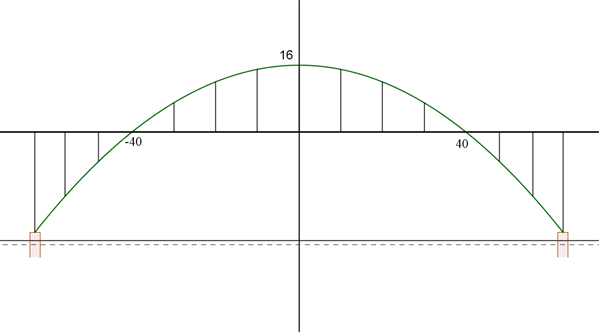
Figur 2 Tværsnit af gennemsejlingsfag

Koordinat­systemets x-akse flugter med kørebanens underside, og buen er symmetrisk omkring koordinatsystemets y-akse.

Buen kan beskrives ved et andengradspolynomium. Buens toppunkt har y-værdien 16 m, og buen skærer x-aksen ved hhv. +40 m og – 40 m.

a)   Bestem en forskrift for buen. 

Vi aflæser af figur 2, at $y_T = 16$ m, $y_1 = 0$ m og $x_1 = 40$ m.
Dermed er forskriften for buen: $y = \dfrac{-16}{40^2}\cdot x^2 + 16 = \:– 0,01\cdot x^2 + 16$

Det oplyses, at gennemsejlingshøjden (forstået som afstanden fra vandoverfladen ved normal vandstand til undersiden af kørebanen) er 26 m, og at oversiden af buens fundamenter er 2 m over vandoverfladen ved normal vandstand.

b)   Bestem buens spændvidde, dvs. afstanden mellem buens understøt-­
      ningspunkter på de to fundamenter (i meter) afrundet til én decimal.

Vi beregner y-værdien ved understøtningspunkterne: $y_u = \:– 26 + 2 = \:–24$ m. Dette indsættes i forskriften, der løses mht. x: 
$– 0,01\cdot x_u^2 + 16 = \:–24$, hvilket giver: $x_u = \sqrt{4000} = 63,25$ m,
og buens spændvidde er derfor $2\cdot 63,25$ m $=126,5$ m.