Lige og ulige funktioner
Lige funktioner
En lige funktion er i princippet en funktion, der kan spejlvendes i y-aksen. Det vil sige, at enhver y-værdi i funktionen har to tilhørende x-værdier, der har samme værdi, men modsat fortegn. Matematisk kan dette beskrives som:
\(f(x)=f(-x)\)
Et eksempel på en lige funktion er \(f(x)=x^2\).
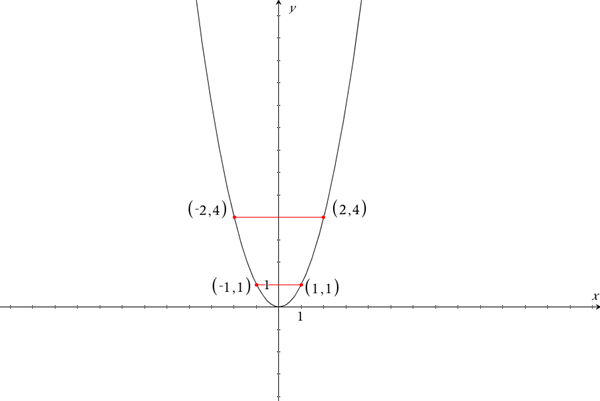
I funktionen \(f(x)=x^2\) har alle y-værdier to tilhørende x-værdier, givet at y-værdien ligger inden for funktionens værdimængde. Værdimængden betegner alle mulige funktionsværdier.
Hvis vi kigger på funktionsværdien \(f(x)=4\), har denne de to tilhørende x-værdier \(x=2\) og \(x=-2\). Samme forhold gør sig gældende for alle funktionsværdierne i \(f(x)=x^2\), og derfor er det en lige funktion.
Andre eksempler på lige funktioner kunne være: \(f(x)=x^4\) og \(f(x)=cos(x)\)
Eksempler
Når vi skal undersøge om en funktion er lige eller ej kan vi benytte definitionen \(f(x)=f(-x)\). Vi kan igen tage \(f(x)=x^2\) som eksempel. Hvis denne funktion er lige, skal den opfylde \(f(x)=f(-x)\). Vi kan nu indsætte vores funktion, og finde ud af om dette er tilfældet. Vi indsætter derfor først \(f(x)=x^2\).
\(f(-x)=x^2\)
På venstre side står der, at vi skal indsætte \(-x\) i vores funktion \(f(x)=x^2\).
\((-x)^2=x^2\)
Uanset hvilken værdi, vi nu vælger for \(x\), vil venstresiden blive positiv, da ethvert reelt tal i anden giver en positiv værdi. Selv en negativ x-værdi vil gøre venstresiden positiv, da produktet af to negative tal altid er positivt. Derfor får vi:
\(x^2=x^2\)
Dette går altså op, og derfor opfylder funktionen \(f(x)=x^2\) vores krav for lige funktioner.
Vi kan også undersøge \(f(x)=cos(x)\): Ligesom før kan vi indsætte vores funktion i \(f(x)=f(-x)\), og undersøge om vores funktion er lige:
\(\cos(x)=\cos(-x)\)
Om cosinus ved vi dog, at enhver værdi \(x\) indsat i cosinus, har den samme værdi som den negerede værdi \(-x\). Udsagnet \(\cos(x)=\cos(-x)\) passer derfor. På grafen herunder ser vi også hvorfor.
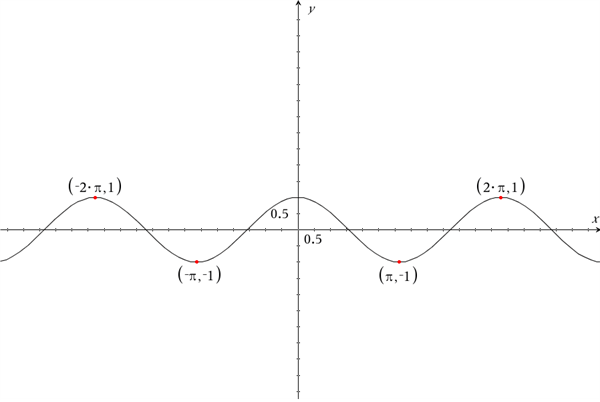
Uanset hvilken værdi, du vælger for \(x\), vil den negerede værdi \(-x\) have samme y-værdi. \(f(x)=\cos(x)\) opfylder derfor vores krav for lige funktioner.
Ulige funktioner
En ulige funktion er en funktion, der er symmetrisk ift. origo. Det betyder, at den kan spejlvendes først i den ene akse og derefter i den anden. Det vil sige, at for ethvert punkt (x,y) er der et tilsvarende punkt (-x,-y) med samme x- og y- værdier - bare med omvendt fortegn. Når dette er tilfældet, kaldes funktionen for ulige. Matematisk beskrives det som:
\(-f(x)=f(-x)\)
Et eksempel på en ulige funktion er: \(f(x)=x^3\)
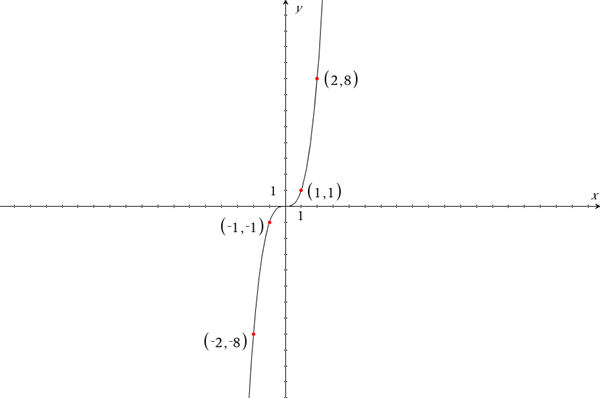
I funktionen \(f(x)=x^3\) finder vi blandt andet punktet (1,1). Hvis funktionen skal være ulige må der derfor også findes et punkt (-1,-1), hvilket der gør. Da denne sammenhæng gør sig gældende for alle reelle tal, må funktionen altså være ulige. For ethvert koordinat \((x,y)\) er der altså et tilsvarende koordinat \((-x,-y)\) med samme værdier for \(x\) og \(y\). Generelt kan det siges, at alle funktioner på formen \(f(x)=x^n\), hvor n er et ulige tal, giver anledning til en ulige funktion.
Andre eksempler på ulige funktioner kunne være: \(f(x)=x\), \(f(x)=x^5\) og \(f(x)=\sin(x)\).
Eksempler
Vi kan teste om funktionen \(f(x)=x^3\) er en ulige funktion ved, at indsætte den i udtrykket \(-f(x)=f(-x)\).
\(-f(x)=-x^3\)
Da vi ved, at \(f(x)=x^3\) kan vi nu sætte den negerede værdi ind på venstresiden
\(-x^3=-x^3\)
Dette udtryk går altså op, og derfor må \(f(x)=x^3\) være en ulige funktion.
Vi kan også tjekke om \(f(x)=\sin(x)\) er en ulige funktion. Vi indsætter først vores funktion i definitionen for ulige funktioner.
\(\-sin(x)=\sin(-x)\)
Ligesom det var tilfældet ved funktionen for cosinus går dette også op, selvom det måske ikke ser sådan ud ved første blik.
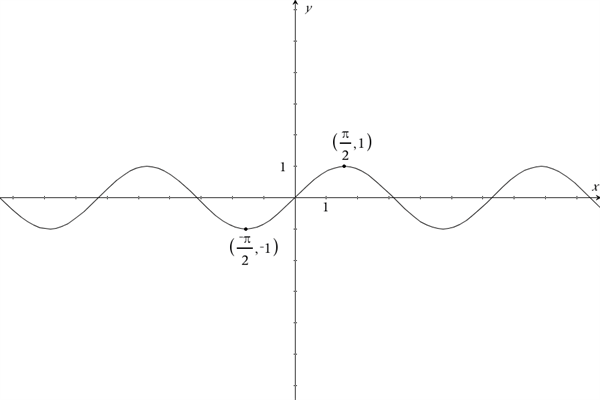
På grafen ovenfor kan vi se, at \(f(\frac{\pi}{2})=1\). Ifølge udtrykket bør den negerede x-værdi \(-\frac{\pi}{2}\) give samme værdi for \(f(x)\), men med modsat fortegn. Vi forventer derfor at: \(f(-\frac{\pi}{2})=-1\). Dette udsagn passer, og det kan vi også se på grafen. Vi kan lave samme test for alle x-værdier, og de vil alle gå op. \(f(x)=sin(x)\) er derfor en ulige funktion.
Andre eksempler
Indtil videre har du stiftet bekendskab med et par lige og ulige funktioner. Det er dog langtfra altid, at en funktion er enten lige eller ulige. En funktion, der er hverken lige eller ulige, er \(f(x)=ln(x)\).
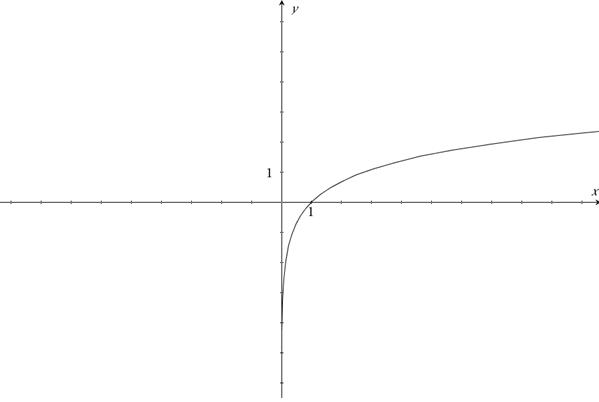
Vi kan se, at funktionen har grænseværdien 0 for y. Det er derfor ikke muligt, at sætte negative \(x\)-værdier eller 0 ind i denne funktion.
Et eksempel på en funktion, der kunne være både lige og ulige er \(f(x)=0\). Når vi indsætter denne funktion i udtrykkene for lige- og ulige funktioner vil det gå op i begge tilfælde. \(f(x)=0\) er derfor både en lige- og en ulige funktion.
Eksempel
Vi vil teste om funktionen \(f(x)=2x+1\) er lige eller ulige. Vi tester først om den er lige. Hvis \(f(x)\) skal være lige må det passe at \(f(x)=f(-x)\). Vi indsætter nu funktionen, og finder ud af om det passer.
\(2x+1=2(-x)+1\)
Vi ser, at det ikke går op, da det første led af forskellige fortegn på hver side af lighedstegnet. Vi kan nu i stedet teste om \(f(x)\) er en ulige funktion. Hvis \(f(x)\) skal være ulige må det passe at \(-f(x)=f(-x)\). Vi indsætter nu funktionen, og finder ud af om det passer.
\(-(2x+1)=2(-x)+1\)
Vi kan omskrive dette udtryk
\(-2x-1=-2x+1\)
Igen ser vi, at det ikke går op, og vi må derfor konkludere at \(f(x)\) hverken er lige eller ulige.
Videolektion
I denne videolektion fortæller Christian om lige og ulige funktioner. Han viser bl.a. at funktioner, der hverken er lige eller ulige, er bygget op af en lige og en ulige del.
