Implicit differentiation
For en lang række eksplicitte funktioner \(y=f(x)\) er der simple regler for differentiation, f.eks. n’te grads polynomier, de trigonometriske funktioner og mange andre. Ved sædvanlig differentiation bestemmer vi \(f’(x)\), som er en forskrift til – for en vilkårlig værdi af \(x\) – at beregne grafens hældning og dermed også hældningen for tangenten til grafen for \(f(x)\).
Hvis der er tale om implicitte funktioner, må vi gribe differentiation lidt anderledes an. Ved en implicit funktion forstår vi en forskrift, der ikke er givet på den eksplicitte form ved \(y=f(x)\), men derimod ved enten \(x=f(y)\) eller \(f(x,y)\).
Som altid, når vi taler differentiation, husker vi på, at differentialkvotienten \(\dfrac{dy}{dx}\) angiver hældningen for tangenten til grafen. Ved implicit differentiation tilvejebringer vi et regneudtryk for \(\dfrac{dy}{dx}\) uden at kende den eksplicitte funktion \(y=f(x)\).
Implicit differentiation illustreres bedst gennem konkrete eksempler.
Eksempel 1
Cirklen med centrum i Origo (0,0) og radius \(r\) er som bekendt givet ved ligningen: \(x^2+y^2=r^2\), se figur 1.
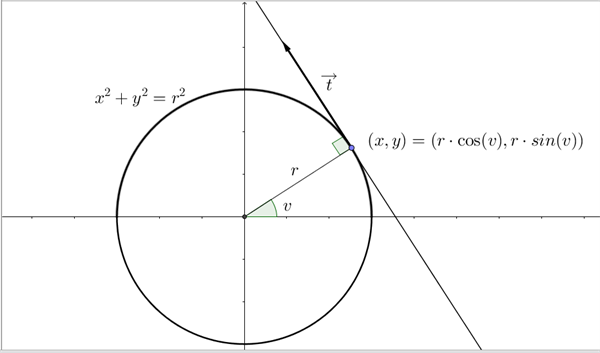
Figur 1 Cirklen, \(x^2+y^2=r^2\)
Hvis vi i cirklens ligning opfatter \(y\) som \(y(x)\) og differentierer på begge sider af lighedstegnet med hensyn til \(x\), får vi:
\(2x + 2y\cdot\dfrac{dy}{dx} = 0\implies \dfrac{dy}{dx} = \dfrac{-x}{y}, y\neq 0\)
Overalt på cirklen (bortset fra ved skæringspunkter med x-aksen) kan vi altså beregne tangentens hældning ved udtrykket \(\dfrac{-x}{y}\). Ved cirklens skæringspunkter med x-aksen er tangenten lodret, og for lodrette linjer er hældningen som bekendt ikke defineret, så begrænsningen \(y\neq 0\) giver god mening og udgør ikke en reel indskrænkning.
Samme resultat for tangentens hældning kan vi komme frem til ved en anden betragtning. Hvis vi - som vist i figur 1 - beskriver punkterne \((x,y)\) på cirkelperiferien ved vinklen \(v\), som radius til punktet danner med x-aksen, er \((x,y) = (r\cdot \cos{v}, r\cdot \sin{v})\). Tangenten til cirklen står vinkelret på radius, og en retningsvektor for tangenten finder vi dermed ved f.eks. at dreje radius 90 \(^\circ\) mod uret:
\(\overrightarrow{t} = (-y, x) = (-r\cdot \sin{v}, r\cdot \cos{v}) = -r\cdot \sin{v}\cdot (1,\dfrac{-r\cdot \cos{v}}{r\cdot \sin{v}})\)
\(= -r\cdot \sin{v}\cdot (1, \dfrac{-x}{y})\)
Denne vektor ses netop at have hældningen \(\dfrac{-x}{y}\), hvilket den implicitte differentiation også førte frem til.
Eksempel 2
Lad sammenhængen mellem \(x\) og \(y\) være givet ved forskriften \(x = \sin{y}, 0\leq y\leq 2\pi\), som vist i figur 2.
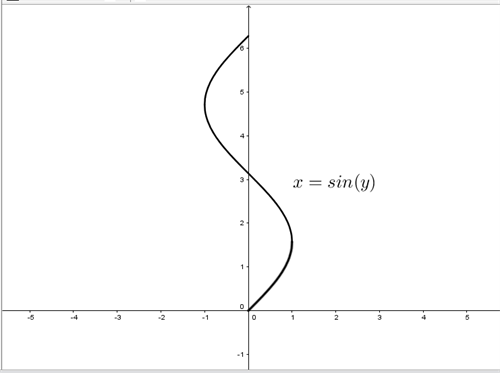
Figur 2 Lodretstående sinuskurve \(x = \sin{y}, 0\leq y\leq 2\pi\)
Hvis vi i forskriften opfatter \(y\) som \(y(x)\) og differentierer på begge sider af lighedstegnet med hensyn til \(x\), får vi:
\(1 = \cos{y}\cdot \dfrac{dy}{dx} \implies \dfrac{dy}{dx} = \dfrac{1}{\cos{y}}, 0\leq y\leq 2\pi\) og \(y\neq \dfrac{\pi}{2},\dfrac{3\pi}{2}\)
Overalt på grafen (bortset fra ved y-værdierne \(\dfrac{\pi}{2}\) og \(\dfrac{3\pi}{2}\)) kan vi beregne tangentens hældning ved udtrykket \(\dfrac{1}{\cos{y}}\). Ved de to anførte y-værdier er tangenten lodret, hvor hældningen ligesom før ikke er defineret.
Eksempel 3
En liggende parabel, som skærer y-aksen i både 2 og 4 og har toppunkt i (-1,3), kan beskrives ved forskriften: \(x = (y - 2)\cdot (y - 4) = y^2 – 6y + 8\), se figur 3.
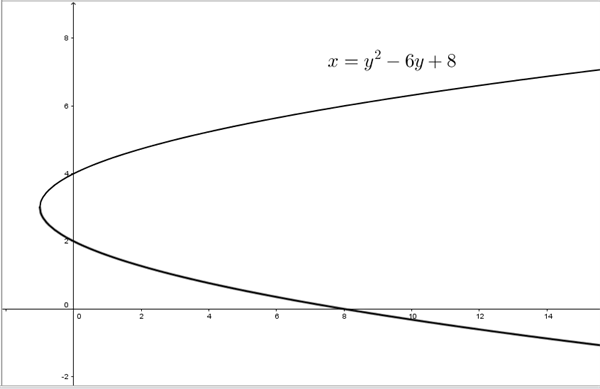
Figur 3 Liggende parabel \(x = y^2 – 6y + 8\)
Hvis vi i forskriften opfatter \(y\) som \(y(x)\) og differentierer på begge sider af lighedstegnet med hensyn til \(x\), får vi:
\(1 = 2y\cdot \dfrac{dy}{dx} – 6\cdot \dfrac{dy}{dx} \implies \dfrac{dy}{dx} = \dfrac{1}{2y-6}, y\neq 3\)
Overalt på den liggende parabel (bortset fra ved \(y = 3\), hvor tangenten er lodret) kan vi beregne tangentens hældning ved udtrykket \(\dfrac{1}{2y-6}\). Heraf ser vi f.eks., at hældningen for parablens tangent er –1, når \(y = 2,5\), og +1, når \(y = 3,5\).
