Areal af parallelogram/ trekanter udspændt af to vektorer
I et koordinatsystem har vi givet to vektorer \(\overrightarrow{a}(x_1,y_1)\) og \(\overrightarrow{b}(x_2,y_2)\). Dem afsætter vi med udgangspunkt i punkt \(A(x_0,y_0)\), se figuren. Vektorerne udspænder et parallelogram \(ABCD\), som er sammensat af to kongruente (dvs. identiske) trekanter \(ABD\) og \(CDB\).
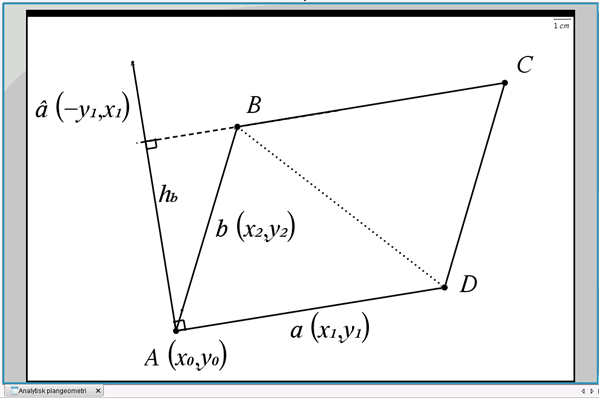
Figur Parallelogram/trekanter udspændt af to vektorer i planen
Vi er interesserede i at bestemme arealet af parallelogrammet \(ABCD\) og af hver trekant. Vi kan se, at tværvektoren til vektor \(\overrightarrow{a}(x_1,y_1)\) er givet ved \(\overrightarrow{\hat{a}}(-y_1,x_1)\). Tværvektoren er også vist i figuren med afsæt i punkt \(A\).
Af figuren ses det, at højden \(h_b\) i parallelogrammet er lig med længden af projektionen af vektor \(\overrightarrow{b}\) på tværvektoren \(\overrightarrow{\hat{a}}\). Vi bruger vores viden om vektorer i planen og sammenhængen mellem to vektorers prikprodukt og længden af den ene vektors projektion på den anden vektor:
\(h_b=\dfrac{|\overrightarrow{b}\cdot \overrightarrow{\hat{a}}|}{ |\overrightarrow{\hat{a}}|}=\dfrac{|x_2\cdot (-y_1)+y_2\cdot x_1|}{|\overrightarrow{\hat{a}}|}=\dfrac{|x_1\cdot y_2-x_2\cdot y_1|}{|\overrightarrow{\hat{a}}|}\)
hvor \(|…|\) i tælleren indikerer numerisk værdi og \(|…|\) i nævneren indikerer længden af vektoren.
Idet \(|\overrightarrow{\hat{a}}|=\sqrt{y_1^2+x_1^2}=|\overrightarrow{a}|\) og arealet af et parallelogram er produktet af sidelængden og højden får vi:
\(A_{ABCD} = |\overrightarrow{a}|\cdot h_b = |x_1\cdot y_2 – x_2\cdot y_1| = det(\overrightarrow{a},\overrightarrow{b})\)
hvor \(det(\overrightarrow{a},\overrightarrow{b})\) angiver determinanten af vektorerne \(\overrightarrow{a}\) og \(\overrightarrow{b}\). Vi har flere skrivemåder for determinanten:
\(det(\overrightarrow{a},\overrightarrow{b}) = \begin{vmatrix} x_1 & x_2 \\ y_1 & y_2 \end{vmatrix} = |x_1\cdot y_2 – x_2\cdot y_1|\).
Ud fra den midterste skrivemåde er huskereglen for beregning af determinanten: "at gange på kryds og trække fra”.
Trekanterne \(ABD\) og \(CDB\) er kongruente og har derfor samme areal:
\(A_{ABD} = A_{CDB} = \dfrac{1}{2}\cdot det(\overrightarrow{a},\overrightarrow{b}) = \dfrac{1}{2}\cdot |x_1\cdot y_2 – x_2\cdot y_1|\)
