Stigningstal ud fra tangens

Forskriften for en ret linje er som bekendt \(y(x)=ax+b\), hvor \(b\) angiver skæring med y-aksen og \(a\) angiver linjens stigningstal (hældningskoefficient) (se evt. her).

 

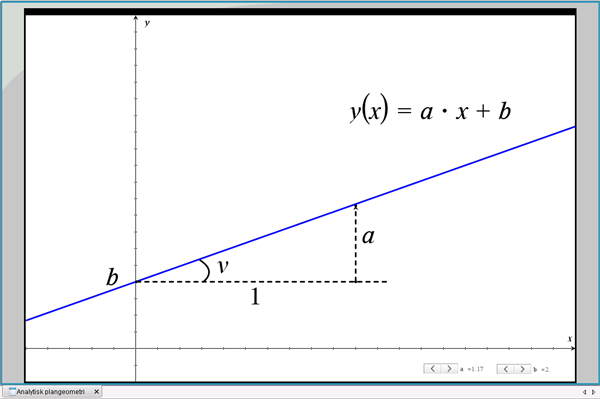
Figur: Stigningstal (hældningskoefficient) for en ret linje

Linjens stigningstal er defineret som ”stigningen i y-værdi, når x-værdien vokser med 1”. Hvis vi kender den vinkel (\(v\)), som den rette linje danner med en vandret linje, kan vi beregne stigningstallet:

\(a=\tan(v)\)           og dermed er:           \(y(x)=\tan(v)\cdot x+b\)

Her har vi udnyttet vores barnelærdom om de trigonometriske funktioner i en retvinklet trekant: ”Tangens til en vinkel er lig med modstående katete (her \(a\)) divideret med hosliggende katete (her 1)”.

Taleksempler:
\begin{matrix}
Vinkel          & Stigningstal                            & Forskrift \\
0^\circ & \tan(v)=0 & y=b \\
30^\circ & \tan(v)=\frac{1}{\sqrt{3}}=0,577 & y(x)=0,577\cdot x+b \\
45^\circ & \tan(v)=1 & y(x)=x+b \\
60^\circ & \tan(v)=\sqrt{3}=1,732 & y(x)=1,732\cdot x+b \\
\end{matrix}