Skalarprodukt (fra cosinus og enhedsvektorer)

Skalarprodukt fra cosinus

Vi ved, at skalarproduktet er givet ved $$\overrightarrow{a}\bullet\overrightarrow{b}=\begin{pmatrix}a_x\\a_y\end{pmatrix}\begin{pmatrix}b_x\\b_y\end{pmatrix}=a_xb_x+a_yb_y$$

Vi kan imidlertid også udtrykke skalarproduktet på en anden måde: $$\overrightarrow{a}\bullet\overrightarrow{b}=\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|\cdot\cos(\theta)$$

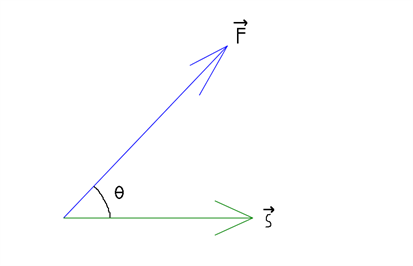
Den nemmeste måde at se, hvorfor dette gælder kommer fra fysikken, hvor arbejde udtrykkes ved "kraft gange vej". $$A=F\cdot\ s$$ Vi kan se på et tilfælde, hvor vi bruger en græsslåmaskine, som beskrevet i følgende billede: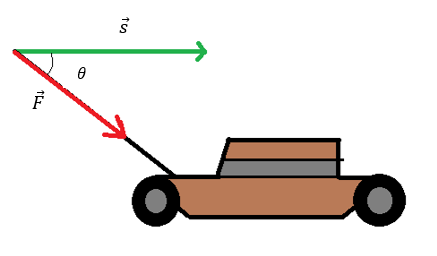 

Vi ønsker at udregne arbejdet, som vi påfører græsslåmaskinen, og den formel er kraft gange vej. Men her er der også en vinkel mellem kraftvektoren F og vejvektoren s. Dvs. at den kraft, som indgår i arbejdet, skal kun være den kraft, som er i vejens retning. Vi skal derfor finde et udtryk for kraftens størrelse i vejens retning ved hjælp af trekantsberegning:  $$\cos(\theta)=\frac{hos}{hyp}\implies hos=hyp \cdot \cos(\theta)=\left|\overrightarrow{F}\right|\cdot \cos(\theta)$$

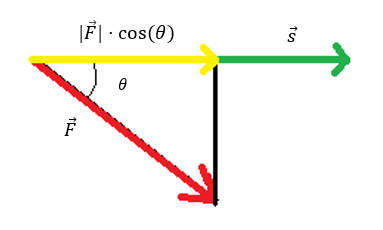
Udtrykket for størrelsen af arbejdet kan nu udtrykkes ud fra størrelsen af kraften i vejens retning og længden af vejvektoren s: $$A=\left|\overrightarrow{F}\right|\cdot\left|\overrightarrow{s}\right|\cdot cos(\theta)$$

Skalarprodukt fra enhedsvektorer:

Vi kan nu forestille os en situation, hvor vi har to enhedsvektorer e_a og e_b med en vinkel theta imellem:

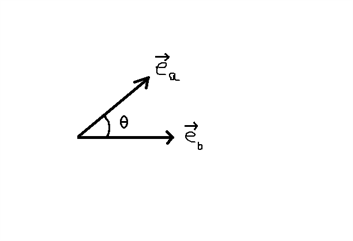Udtrykket bliver forenklet, da enhedsvektorer altid har længden 1, så vi får et skalarprodukt givet ved $$\cos(\theta)=\frac{a_xb_x+a_yb_y}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\frac{e_{ax}e_{bx}+e_{ay}e_{by}}{1\cdot1}=\overrightarrow{e_a}\bullet\overrightarrow{e_b}$$ Dvs. vi kan udtrykke skalarproduktet som $$\overrightarrow{e_a}\bullet\overrightarrow{e_b}=\hat{a}\bullet\hat{b}=\cos(\theta)$$ 

Eksempel 1 - udregne vinkel mellem to vektorer:

Vi skal udregne vinklen mellem to vektorer givet ved $$\overrightarrow{a}=\begin{pmatrix}2\\1\end{pmatrix} \, \, og \, \, \,  \overrightarrow{b}=\begin{pmatrix}3\\4\end{pmatrix}$$ Vi indsætter de oplyste vektorer ind i vores formel og regner løs $$\overrightarrow{a}\bullet\overrightarrow{b}=\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|\cdot\cos(\theta)\implies\cos(\theta)\frac{a_xb_x+a_yb_y}{\sqrt{a^2_x+a^2_y\sqrt{b^2_x+b^2_y}}}$$ $$\cos(\theta)\frac{2\cdot3+1\cdot4}{\sqrt{2^2+1^2\sqrt{3^2+4^2}}}=\frac{2}{\sqrt{5}}$$ $$\implies\theta=25.5^\circ$$

 Eks. 2 - udregne vinkel mellem to enhedsvektorer:

Vi har fået givet to enhedsvektorer $$\hat{a}=\begin{pmatrix}0.24\\0.97\end{pmatrix},\hat{b}=\begin{pmatrix}0.75\\0.66\end{pmatrix}$$ Vi skal udregne vinklem mellem dem. $$\cos(\theta)=0.25\cdot0.75+0.97\cdot0.66=0.82\implies\theta=34.9^\circ$$

Eks. 3 - finde en vektor, som danner en bestemt vinkel med en anden vektor:

Vi får givet en vektor a $$\overrightarrow{a}=\begin{pmatrix}7\\15\end{pmatrix}$$ og vi skal finde en vinkel b, som danner en 25 graders vinkel med vektor a. Vi får desuden at vide, at vektor b har længden 20 og dens x-komponent skal være 9. $$\overrightarrow{a}\bullet\overrightarrow{b}=\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|\cdot\cos(\theta)\implies7\cdot9+15\cdot b_y=\sqrt{7^2+15^2}\cdot20\cdot\cos(25)$$ $$\implies b_y=15.8$$ Nu har vi både x-komponenten og y-komponenten for vektor b $$\overrightarrow{b}=\begin{pmatrix}9\\15.8\end{pmatrix}$$

Industrieksempel - Udregn en kranvogns arbejde              

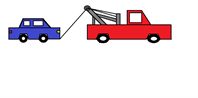En kranvogn skal trække en bil, og vi kan beskrive situationen med følgende tegning, hvor kraftvektorerne er indtegnet:

Vi får oplyst at kraften F har størrelsen 1000 N, strækningen kranvognen trækker bilen er 1000 meter og vinklen mellem kraftvektoren og stedvektoren er 60 grader. Vi vil gerne udregne arbejdet af denne situation.

Formlen for arbejde er (som nævnt tidligere) $$A=\left|\overrightarrow{F}\right|\cdot\left|\overrightarrow{s}\right|\cdot cos(\theta)$$ og her kan vi se, at det bare er skalarproduktet, dvs. $$A=\overrightarrow{a}\bullet\overrightarrow{b}$$

$$A=(1000N)\cdot(1000m)\cdot \cos(60)=5\cdot10^5N\cdot m=5\cdot10^5J=500kJ$$