Projektion (fra enhedsvektor)

 Projektion generelt:

Vi ved, at en vektor kan projiceres ind på en linje eller på en anden vektor. Længden af en vektor a projiceret ind på en anden vektor b er $$\left|\overrightarrow{a}_{\overrightarrow{b}}\right|=\frac{\left|\overrightarrow{a}\bullet\overrightarrow{b}\right|} {\left|\overrightarrow{b}\right|}$$ og selve vektoren er givet ved $$\overrightarrow{a}_{\overrightarrow{b}}=\frac{\overrightarrow{a}\bullet\overrightarrow{b}}{\left|\overrightarrow{b}\right|^2}\bullet\overrightarrow{b}$$ Her er der vist en projektion af vektor a på vektor b:

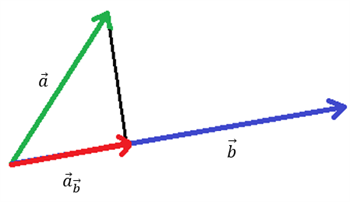
Og selvfølgelig gælder det også omvendt, at hvis det var vektor b projiceret på vektor a i stedet for:  $$\left|\overrightarrow{b}_{\overrightarrow{a}}\right|=\frac{\left|\overrightarrow{a}\bullet\overrightarrow{b}\right|}{\left|\overrightarrow{a}\right|} \, \, \, og \, \, \,   \overrightarrow{b}_{\overrightarrow{a}}=\frac{\overrightarrow{a}\bullet\overrightarrow{b}}{\left|\overrightarrow{a}\right|^2}\bullet\overrightarrow{a}$$

Projektion fra enhedsvektor:

Vi ved, at man kan lave en vilkårlig vektor om til en enhedsvektor med formlen $$\overrightarrow{e}=\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|} \, \, \,  eller \, \, \, \hat{b}=\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}$$

Vi omskriver vores projektionsformel, så vi får et udtryk, hvor enhedsvektoren for vektor b indgår:

$$\overrightarrow{a}_{\overrightarrow{b}}=\frac{\overrightarrow{a}\bullet\overrightarrow{b}}{\left|\overrightarrow{b}\right|^2}\cdot\overrightarrow{b}=\frac{\overrightarrow{a}\bullet\overrightarrow{b}}{\left|\overrightarrow{b}\right|}\cdot\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}=\left|\overrightarrow{a_{\overrightarrow{b}}}\right|\cdot\hat{b}$$ og ligeledes $$\overrightarrow{b}_{\overrightarrow{a}}=\left|\overrightarrow{b_{\overrightarrow{a}}}\right|\cdot\hat{a}$$  Dette giver også en god mening, hvis man ser, at enhedsvektoren er retningsangivende for projektionen.

Eksempel 1 - projektion uden og med brug af enhedsvektorer:

Vi har to vektorer a og b:

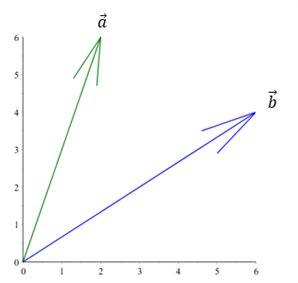
Vektor a skal projiceres på vektor b. Vi kan løse dette problem med og uden brug af enhedsvektorer:

Uden enhedsvektorer:

Her skal følgende formler bruges: $$\left|\overrightarrow{a}_{\overrightarrow{b}}\right|=\frac{\left|\overrightarrow{a}\bullet\overrightarrow{b}\right|}{\left|\overrightarrow{b}\right|} \, \, \, og \, \, \, \overrightarrow{a}_{\overrightarrow{b}}=\frac{\overrightarrow{a}\bullet\overrightarrow{b}}{\left|\overrightarrow{b}\right|^2}\cdot\overrightarrow{b}$$ Først udregnes længden af projektionen $$\left|\overrightarrow{a}_{\overrightarrow{b}}\right|=\frac{\left|\overrightarrow{a}\bullet\overrightarrow{b}\right|}{\left|\overrightarrow{b}\right|}=\frac{\left|a_xb_x+a_yb_y\right|}{\sqrt{(b_x)^2+(b_y)^2}}$$ $$\implies \left|\overrightarrow{a}_{\overrightarrow{b}}\right|=\frac{\left|2 \cdot 6+6\cdot 4\right|}{\sqrt{(6)^2+(4)^2}}=5$$

Herfefter udregnes selve vektoren $$\overrightarrow{a}_{\overrightarrow{b}}=\frac{\overrightarrow{a}\bullet\overrightarrow{b}}{\left|\overrightarrow{b}\right|^2}\cdot\overrightarrow{b}=\frac{a_xb_x+a_yb_y}{(b_x)^2+(b_y)^2}\cdot\overrightarrow{b}$$

$$\implies \overrightarrow{a}_{\overrightarrow{b}}=\frac{(2)\cdot(6)+(6)\cdot(4)}{(6)^2+(4)^2}\cdot\begin{pmatrix}6\\4\end{pmatrix}=0.69\cdot\begin{pmatrix}6\\4\end{pmatrix}=\begin{pmatrix}4.14\\2.76\end{pmatrix}$$

Med enhedsvektorer:

Her skal følgende formler bruges:$$\hat{b}=\frac{\overrightarrow{b}}{{\left|\overrightarrow{b}\right|}} \, \, \,  , \, \, \, \left|\overrightarrow{a}_{\overrightarrow{b}}\right|=\frac{\left|\overrightarrow{a}\bullet\overrightarrow{b}\right|}{\left|\overrightarrow{b}\right|} \, \, \,   og \, \, \,   \overrightarrow{a}_{\overrightarrow{b}}=\left|\overrightarrow{a}_{\overrightarrow{b}}\right|\cdot\hat{b}$$

Længden af projektionen udregnes på samme måde som i "uden enhedsvektorer". Dvs. vi får igen $$\left|\overrightarrow{a}_{\overrightarrow{b}}\right|=5$$ Nu skal vektoren b laves om til en enhedsvektor: $$\hat{b}=\frac{\begin{pmatrix}6\\4\end{pmatrix}}{\sqrt{(6)^2+(4)^2}}=\frac{\begin{pmatrix}6\\4\end{pmatrix}}{7.21}=\begin{pmatrix}\frac{6}{7.21}\\\frac{4}{7.21}\end{pmatrix}=\begin{pmatrix}0.83\\0.55\end{pmatrix}$$ Det indsætter vi nu i vores sidste formel $$\overrightarrow{a}_{\overrightarrow{b}}=5\cdot\begin{pmatrix}0.83\\0.55\end{pmatrix}=\begin{pmatrix}4.14\\2.76\end{pmatrix}$$

Eksempel 2 - projektion med enhedsvektorer

Vi skal projicere vektor d på vektor c. Dette skal løses med enhedsvektormetoden. Vi får oplyst, at vektorne er givet ved: $$\overrightarrow{c}=\begin{pmatrix}-6\\-6\end{pmatrix} \, \, \, og \, \, \,  \overrightarrow{d}=\begin{pmatrix}6\\2\end{pmatrix}$$

                                                                                     

Vi skal først lave vektor c om til en enhedsvektor, så vi kan bruge formlen $$\overrightarrow{b}_{\overrightarrow{a}}=\left|\overrightarrow{b_{\overrightarrow{a}}}\right|\cdot\hat{a}$$ Dette gøres ved $$\hat{c}=\frac{\overrightarrow{c}}{\left|\overrightarrow{c}\right|}\implies \hat{c}=\frac{\begin{pmatrix}-6\\-6\end{pmatrix}}{\sqrt{(-6)^2+(-6)^2}}=\begin{pmatrix}\frac{-6}{8.48}\\\frac{-6}{8.48}\end{pmatrix}=\begin{pmatrix}-0.707\\-0.707\end{pmatrix}$$ Nu skal længden af projektionen udregnes. $$\left|\overrightarrow{d}_{\overrightarrow{c}}\right|=\frac{\left|\overrightarrow{d}\bullet\overrightarrow{c}\right|}{\left|\overrightarrow{c}\right|}\rightarrow \left|\overrightarrow{d}_{\overrightarrow{c}}\right|= \frac{\left|6\cdot(-6)+2\cdot(-6)\right|}{\sqrt{(-6)^2+(-6)^2}}=\frac{48}{8.48}=5.66$$ Nu kan vi indsætte det i vores første formel og få vektor d's projektion på vektor c:

$$\overrightarrow{d}_{\overrightarrow{c}}=\left|\overrightarrow{d}_{\overrightarrow{c}}\right|\cdot\hat{c}\rightarrow \overrightarrow{d}_{\overrightarrow{c}}=5.66\cdot\begin{pmatrix}-0.707\\-0.707\end{pmatrix}=\begin{pmatrix}-4\\-4\end{pmatrix}$$

Industrieksempel - Kraftvektor projiceres i ny retning:

Et fly har en autopilot, som ønsker at forudsige et retningsskifte for flyvet. Vi kalder den nuværende retning for F₁  (betegner kraftvektoren i den retning) og den nye retning for r-vektor.

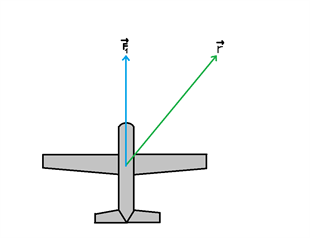
Autopilot-programmet kender den nuværende retning (og størrelse), som er givet ved $$\overrightarrow{F_1}=\begin{pmatrix}0\\2000\end{pmatrix}N  \,  \, \,  og \, \, dvs. \, \,  |\overrightarrow{F_1}|=2000N$$  Den nye retning, r, kender programmet også, og den er givet ved $$\overrightarrow{r}=\begin{pmatrix}150\\200\end{pmatrix}m$$ Vi kan nu prøve at udregne projektionen af F₁ på r, som autoprogrammet skal udregne for at det kan forudsige flyets nye kraftvektor.

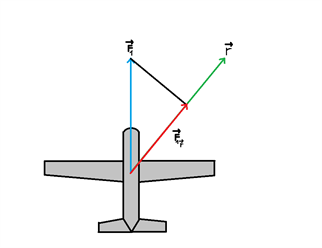
Vi kan dog se, at vores enheder bliver forkerte, hvis vi ganger en kraftvektor (målt i N) med retningsvektor (målt i meter), og desuden vil vores tal generelt blive helt forkerte. Derfor skal vi først lave retningsvektoren om til en enhedsvektor, så den kun angiver den specifikke retning for den projicerede vektor (se mere i enhedsvektor-sektionen): $$\hat{r}=\frac{\overrightarrow{r}}{|\overrightarrow{r}|}\implies \hat{r}=\frac{\begin{pmatrix}150\\200\end{pmatrix}m}{\sqrt{(150m)^2+(200m)^2}}=\frac{\begin{pmatrix}150\\200\end{pmatrix}m}{250m}=\begin{pmatrix}\frac{150}{250}\\\frac{200}{250}\end{pmatrix}=\begin{pmatrix}0.60\\0.80\end{pmatrix}$$ Nu kan vi først finde størrelsen af vores projektion med formlen $$\left|\overrightarrow{F_1}_{\hat{r}}\right|=\frac{\left|\overrightarrow{F_1}\bullet\hat{r}\right|} {\left|\hat{r}\right|}=\left|\overrightarrow{F_1}\bullet\hat{r}\right|$$ $$\rightarrow\left|\overrightarrow{F_1}_{\hat{r}}\right|=0\cdot0.60+2000N\cdot 0.80=1600N$$ Da vi har størrelsen af projektionen kan retningsændringen til sidst udregnes med formlen $$\overrightarrow{F_1}_{\overrightarrow{r}}=\left|\overrightarrow{F_1{_{\overrightarrow{r}}}}\right|\cdot\hat{r}$$ $$\implies \overrightarrow{F_1}_{\overrightarrow{r}}=1600N \cdot\begin{pmatrix}0.60\\0.80\end{pmatrix}=\begin{pmatrix}960\\1280\end{pmatrix}N$$