Andengradsuligheder

Du har tidligere arbejdet med andengradsligninger, som typisk kan skrives på formen:

\(ax^2 + bx + c = 0\)

For at løse ligningen kan du formentlig genkende formlen: \(d=b^2-4\cdot a\cdot c\) til bestemmelse af diskriminanten, og derefter løses andengradsligningen ved: \(x = \frac{-b\: \pm\: \sqrt{d}}{2a}\)

Andengradsuligheder adskiller sig fra andengradsligningen ved, at ligheds-tegnet erstattes af et ulighedstegn. Der er fem forskellige ulighedstegn at vælge imellem:

\(ax^2 + bx + c \ne 0\)          hvor "\(\ne\)" læses som "er forskellig fra"

\(ax^2 + bx + c > 0\)          hvor ">" læses som "er større end "

\(ax^2 + bx + c \geq 0\)          hvor "\(\geq\)" læses som "er større end eller lig med"

\(ax^2 + bx + c < 0\)          hvor "<" læses som "er mindre end"

\(ax^2 + bx + c \leq 0\)          hvor "\(\leq\)" læses som "er mindre end eller lig med"

Alle disse tilfælde løses ved først at løse den sædvanlige andengradsligning \(ax^2 + bx + c = 0\) og derefter finde intervallerne, hvor uligheden passer.

Eksempel

Der er givet andengradsuligheden  \(2x^2 + 2x - 4 \geq 0\). Først løser vi andengradsligningen \(2x^2 + 2x - 4 = 0\). Vi starter med at bestemme diskriminanten:

\(d = 2^2 - 4\cdot 2\cdot (-4)\)

\(d = 36\)

Nu kan vi så bestemme rødderne eller nulpunkterne:

\(x=\frac{-2\: \pm\: \sqrt{36}}{2\: \cdot\: 2}\)

\(x_1 = 1 \wedge x_2 = -2\)

For at løse andengradsuligheden er det en rigtig god ide at tegne eller skitsere grafen for andengradspolynomiet \(f(x) = 2x^2 + 2x - 4\):

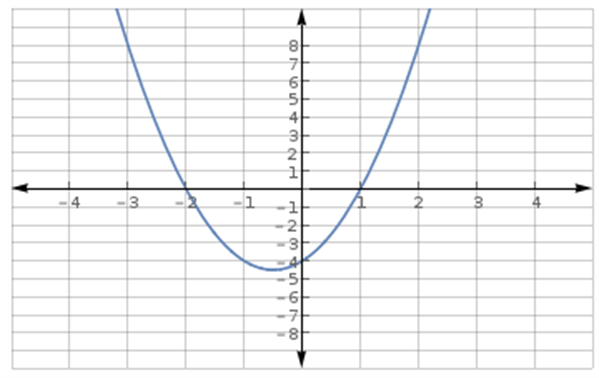
For at løse andengradsuligheden \(2x^2 + 2x - 4 \geq 0\) søger vi de x-værdier, der gør, at værdien af venstresiden bliver større end eller lig med 0. Ud fra grafen kan vi se, at værdien af venstresiden er mindre end 0, hvis x ligger i intervallet mellem -2 og 1. Løsningen til andengradsuligheden er derfor alle de x-værdier, der ligger udenfor dette interval:

$$L = \{ x \in \mathbb{R} | -\infty < x \leq -2 \vee 1 \leq x < \infty \}$$