Introduktion til cosinus og sinus
Her definerer vi funktionerne \(\cos\) og \(\sin\) og beskriver sammenhængen mellem grader og radianer.
Cosinus og sinus
Betragt cirklen nedenfor med centrum i origo, altså \( (0,0) \) , og radius \( 1 \). Denne specifikke cirkel kaldes enhedscirklen. Det smarte ved cirkler er, at alle punkterne, der ligger på cirklen, har samme afstand til dens centrum. Det vil sige at enhedscirklen består af de punkter, hvor afstanden fra punktet til \( (0,0) \) er \( 1 \).
Et punkt \( P = (x,y) \) ligger dermed på enhedscirklen, når afstanden fra punktet til origo er lig med \( 1 \). Ifølge Pythagoras er dette præcist, når
$$ x^2 + y^2 = 1^2 = 1 $$
Betragt figuren nedenfor: Punktet \( P = (x_0 , y_0) \) ligger på enhedscirklen.
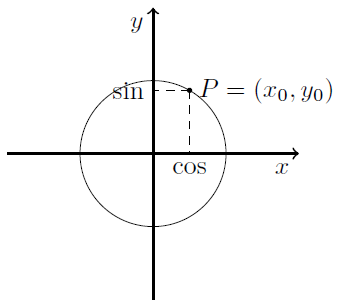
Definition: Hvis et punkt \( P = (x_0 , y_0) \) ligger på enhedscirklen, defineres
$$ \cos ( P ) = x_0 $$
$$ \sin ( P ) = y_0 $$
Med andre ord, hvis du har et punkt, der ligger på enhedscirklen, er \( \cos \) til punktet lig med \( x \) - værdien for punktet, mens \( \sin \) er lig \( y \)- værdien for punktet.
Eksempel: Betragt punktet \( P = \left( \frac{1}{2} , \frac{\sqrt{3}}{2} \right) \). Lad os først tjekke, om punktet ligger på enhedscirklen. Ifølge diskussionen ovenfor, er dette, når afstanden til origo er \( 1 \). Vi finder afstanden ved hjælp af Pythagoras:
$$ x^2 + y^2 = \left( \frac{1}{2} \right)^2 + \left( \frac{\sqrt{3}}{2} \right)^2 = \frac{1}{4} + \frac{3}{4} = \frac{4}{4} = 1.$$
Dermed ligger punktet på enhedscirklen. Vi kan nu beregne cosinus og sinus til punktet:
Da \( \cos \) er defineret som \( x \)-værdien for punktet, er
$$ \cos ( P ) = \frac{1}{2} $$
Da \( \sin\) er defineret som \( y \)-værdien for punktet, er
$$ \sin( P ) = \frac{\sqrt{3}}{2} \approx 0,866.$$
En lille bemærkning: Ifølge Pythagoras' læresætning
$$ a^2 + b^2 = c^2 $$
får vi ligheden
$$ \cos(v) ^2+ \sin (v) ^2 = 1^2 = 1.$$
Denne lighed går tit under det ikke særligt flatterende navn, idiotformlen.
Grader og radianer
Nu har vi defineret, hvad vi mener med cosinus og sinus. Nu skal vi koble disse to begreber til vinkler. Den mest intuitive måde, vi kan gøre dette på, er, at angive hvilken vinkel punktet har med \( x \)-aksen, se figuren nedenfor.
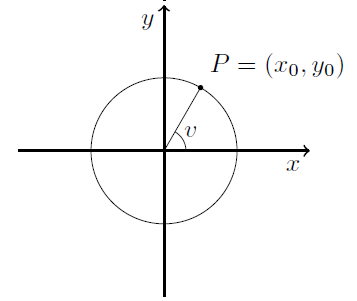
Her er markeret det punkt \( P = (x_0 , y_0) \), der har vinklen \( v \) til \( x \)-aksen. Ifølge definitionen ovenfor er
$$ \cos ( v ) = x_0 $$
$$ \sin ( v ) = y_0 $$
Her skal bemærkes, at vi altid regner positive vinkler til at gå imod urets omløbsretning (positiv omløbsretning) og negative vinkler med urets omløbsretning (negativ omløbsretning).
En anden metode er, at angive vinklen i radianer, betragt figuren nedenfor
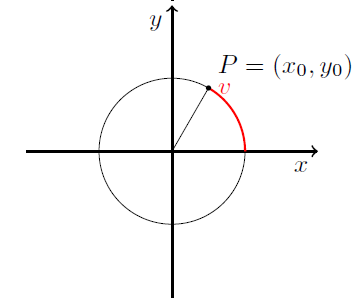
Vinklen angives nu som følger: Stil dig i punktet \( (1,0) \) på enhedscirklen. Bevæg dig afstanden \( v \) langs cirklen. Det punkt, du ender i, er dit punkt \( P \).
Enhedscirklen har radius \( 1 \). Det vil sige, at omkredsen er \( O = 2 \pi \cdot 1 = 2 \pi\). Et helt omløb i cirklen, altså en vinkel, der svarer til \( 360 \) grader, er dermed \( 2 \pi \). Ligeledes svarer \( 90 \) grader, en kvart gang rundt i cirklen, til \( \frac{\pi}{2} \), \( 180 \) grader, en halv gang rundt i cirklen, svarer til \( \pi \) osv.
Omregning fra grader til radianer:
Hvis vi har en vinkel \( v \) i grader, og gerne vil bestemme, hvor mange radianer, det er, gøres det ud fra følgende formel:
$$ r = \frac{v}{360} \cdot 2 \pi $$
Her er \( r \) vinklen i radianer, som vi er på jagt efter.
Lad os prøve at tænke over, hvad denne formel indeholder:
- \( \frac{v}{360} \) svarer til den brøkdel, vi går rundt i cirklen. For eksempel er en \( 90 \) graders vinkel en kvart gang rundt, da
$$ \frac{90}{360} = \frac{1}{4}$$.
- \(2 \pi \) er omkredsen af cirklen, altså hvor langt er der rundt i hele cirklen.
Når vi ganger de to størrelser sammen, finder vi hvor stor en brøkdel af omkredsen, vores vinkel udspænder - det vil præcis sige, hvad vinklen er i radianer.
Eksempel:
Hvor mange radianer svarer \( 90 \) grader til?
Vi bruger formlen \( r = \frac{v}{360} \cdot 2 \pi \)
$$ r = \frac{90}{360} \cdot 2 \pi = \frac{1}{4} \cdot 2 \pi = \frac{\pi}{2}$$.
