Guldins regler

En cirkulær ring, f.eks. et stenhjul, kan betragtes som en cylinder med et hul i midten, se figur 1. Hullet har også form som en cylinder, og de to cylindre (benævnt hhv. den ydre og den indre cylinder) kaldes koncentriske, da de har sammenfaldende længdeakse.

 

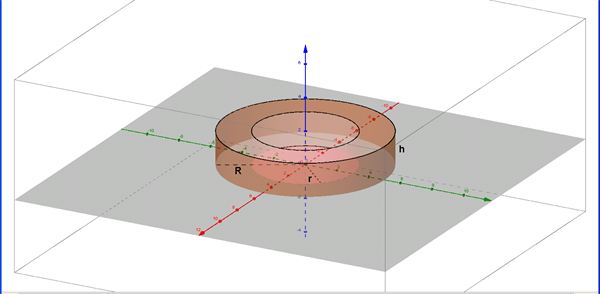
 Figur 1          En cirkulær ring

Rumfanget af den cirkulære ring er forskellen i rumfang for den ydre cylinder og den indre cylinder:

\(V_{ring} = h\cdot (\pi\cdot R^2)-h\cdot (\pi\cdot r^2) = \pi\cdot h\cdot (R^2-r^2)\)

hvor \(R\) er radius i den ydre cylinder, \(r\) er radius i den indre cylinder og \(h\) er ringens højde.

Men vi kan også nå frem til formlen for rumfanget ved en lidt anden betragtning af ringen. Ringens tværsnit er et rektangel med bredden \((R-r)\) og højden \(h\), og altså er ringens tværsnitsareal \(A = h\cdot (R-r)\). Og ringens omkreds målt langs midten af ringens tykkelse er \(O = 2\cdot\pi\cdot a\), hvor \(a\) er middelværdien af de to radier: \(a = \frac{R+r}{2}\). Rumfanget fremkommer ved at gange tværsnitsarealet med omkredsen:

Guldins regel:                   \(V_{ring} = O\cdot A = 2\cdot\pi\cdot a\cdot A\)

som kan omskrives til      \(V_{ring} = 2\cdot\pi\cdot\frac{R+r}{2}\cdot h\cdot (R-r) = \pi\cdot h\cdot (R^2-r^2)\)

Hvis vi skærer et vinkeludsnit af ringen væk, se figur 2, kan den tilbageværende del af ringen karakteriseres ved vinklen, \(v\), hvor \(0<v<360^\circ\) eller \(0<v<2\pi\).

 

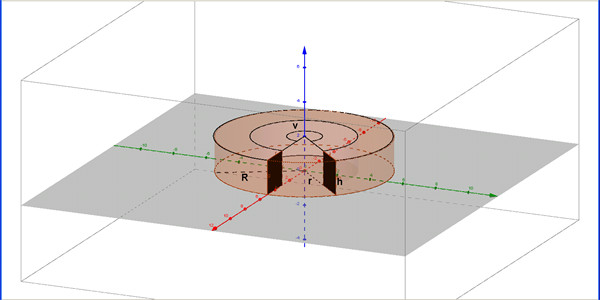
 Figur 2          En cirkulær ring, hvor et vinkeludsnit er skåret væk

Rumfanget af den tilbageværende del af ringen er direkte proportionalt med vinklen, \(v\), og med \(v\) angivet i grader:

Guldins regel giver:                         \(V_{del-ring} = \dfrac{v}{360}\cdot 2\cdot\pi\cdot a\cdot A\)

som kan omskrives til:

Hvis \(v\) angives i grader:                   \(V_{del-ring} = \dfrac{v}{360}\cdot\pi\cdot h\cdot (R^2-r^2)\)

Hvis \(v\) angives i radianer:                \(V_{del-ring} = \dfrac{v}{2}\cdot h\cdot (R^2-r^2)\)

Areal

Guldin havde en lignende regel for tilfældet hvor ringen ikke har et rumfang, men er en flade, det kunne f.eks. være et enkelt bånd i en guirlande. Her findes overfladearealet ved næsten samme metode

Guldins regel:                                       \(O_{A_{del-ring}} = \dfrac{v}{360}\cdot 2 \cdot \pi \cdot R \cdot h\)

Hvor den eneste forskel er, at R nu betegner radius for cirkelfladen og ikke den ydre radius. 

Eksempel

På taget af kunstmuseet ARos i Århus er etableret kunstværket Your Rainbow Panorama – udformet som en cirkulær ring, en rundgang – som man kan gå hele vejen rundt i, og som er skabt af den dansk/islandske kunstner Olafur Eliasson i 2011.

 

Figur 3          Your Rainbow Panorama på ARoS

Rundgangens ydre diameter er 52 m, den indre diameter er 46 m og rundgangens højde er 3 m.

Tværsnittet er kvadratisk, idet bredden af rundgangen er \(\frac{1}{2}\cdot (D-d) = 3\) m, og tværsnitsarealet er derfor \(A = b\cdot h = 3\cdot 3 = 9\) m². Rundgangens omkreds målt langs midten af gangens bredde er \(O = 2\cdot\pi\cdot\frac{R+r}{2}\) \(= 2\cdot\pi\cdot\frac{26+23}{2} = 153,9\) m, og rumfanget er \(V_{ring} = A\cdot O = 9\cdot 153,9\) \(= 1.385\) m³. Samme rumfang kommer man frem til med formlen \(V_{ring} = \pi\cdot h\cdot (R^2-r^2) = \pi\cdot 3\cdot (26^2-23^2)\).

Vi har tidligere regnet på Your Rainbow Panorama - se her.