Skruelinje
En skruelinje er en tredimensionel kurve, der kan opfattes som beliggende på ydersiden af en cylinder, se figur 6. Den sorte skruelinje snor sig om cylinder-ens længdeakse. Når der indlægges et (x,y,z)-koordinatsystem med z-aksen sammenfaldende med cylinderens længdeakse, kan skruelinjen beskrives ved koordinaterne:
\((x(t), y(t), z(t)) = (r\cdot\cos(t), r\cdot\sin(t), \dfrac{h}{2\pi}\cdot t)\)
hvor \(t\) angiver radianer, og \(h\) angiver højden af én vinding langs z-aksen. I figur 6 er x-aksen rød, y-aksen grøn og z-aksen blå. Skruelinjens projektion på (x,y)-planen er en cirkel med radius, \(r\), og centrum i (0,0).
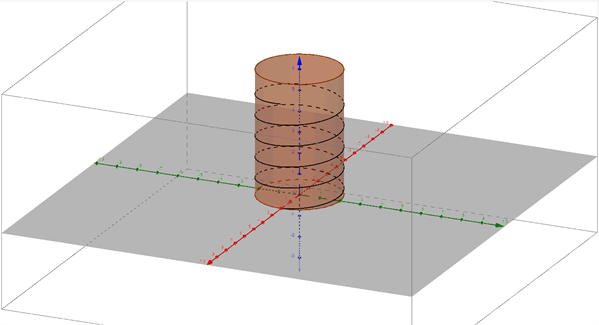
Figur 6 En skruelinje kan opfattes som beliggende på ydersiden af en cylinder
Eksempler på skruelinjer er gevind og fjedre inden for mekanik og DNA-molekyler inden for biologi.
Længden af et infinitesimalt stykke af skruelinjen er:
\(dL = \sqrt{dx^2+dy^2+dz^2} = \sqrt{x’(t)^2+y’(t)^2+z’(t)^2}\cdot dt = \sqrt{r^2+(\dfrac{h}{2\pi})^2}\cdot dt\)
Her har vi benyttet, at \((x’(t), y’(t), z’(t)) = (-r\cdot\sin(t), r\cdot\cos(t), \dfrac{h}{2\pi})\)
og at \((\sin^2(t)+\cos^2(t))=1\).
Ved at integrere \(dL\) over én vinding, dvs. fra \(t=0\) til \(t=2\pi\), finder vi længden af én vinding af skruelinjen:
\(\displaystyle L_1 = \int_{0}^{2\pi} \sqrt{r^2+(\dfrac{h}{2\pi})^2}\:dt = 2\pi\cdot\sqrt{r^2+(\dfrac{h}{2\pi})^2} = 2\pi r\cdot\sqrt{1+(\dfrac{h}{2\pi r})^2}\)
Her bemærker vi, at \(2\pi r\) er omkredsen af en cirkel med radius \(r\), hvilket er længden af én vinding, hvis vi ignorerer vindingens højde. Faktoren under kvadratrodstegnet illustrerer dermed betydningen af vindingens højde for skruelinjens længde, og vi ser, at det er vindingens højde målt i forhold til cirklens omkreds - hvilket vi kunne betegne som den relative højde af en vinding - der er afgørende. Ikke overraskende er sammenhængen, at jo større den relative højde af en vinding er, desto større er indflydelsen på længden af skruelinjen.
Eksempler
Regneeksempel 1:
Bestem længden af en 5 cm høj fjeder bestående af 10 vindinger, hvor diameteren er 0,8 cm.
Først bestemmes højden af én vinding: \(h=\frac{5}{10}=0,5\) cm. Idet radius er: \(r=\frac{d}{2}=0,4\) cm, er længden af fjederen:
\(L = 10\cdot L_1 = 10\cdot 2\pi r\cdot\sqrt{1+(\dfrac{h}{2\pi r})^2} = 20\cdot\pi\cdot 0,4\cdot\sqrt{1+(\dfrac{0,5}{2\cdot\pi\cdot 0,4})^2}\)
\(L = 25,6\) cm
Den relative højde af en vinding er 0,20, og hvis vi ignorerede vindingernes højde, ville vi komme frem til en længde af fjederen på 25,1 cm. Vindingernes højde giver altså her en forøgelse af skruelinjens længde på 2 %.
Regneeksempel 2
Bestem længden af en 56 mm høj fjeder bestående af 8 vindinger, hvor diameteren er 30 mm.
Først bestemmes højden af én vinding: \(h=\frac{56}{8}=7\) mm. Idet radius er \(r=\frac{d}{2}=15\) mm, er længden af fjederen:
\(L = 8\cdot L_1 = 8\cdot 2\pi r\cdot\sqrt{1+(\dfrac{h}{2\pi r})^2} = 16\cdot\pi\cdot 15\cdot\sqrt{1+(\dfrac{7}{2\cdot\pi\cdot 15})^2}\)
\(L = 756\) mm
Den relative højde af en vinding er 0,074, og hvis vi ignorerede vindingernes højde, ville vi komme frem til en længde af fjederen på 754 mm. Vindinger-nes højde giver altså her en forøgelse af skruelinjens længde på kun 0,3 %.
